Solución integrales dobles.
Me puedes ayudar a resolver este ejercicio de integrales dobles
1 respuesta
calcular el volumen del la región limitada por z=h (z>0) y x al cuadrado + y al cuadrado igual a z al cuadrado si me puedes colaborar con la gráfica me ayudarías mucho.pero me piden resolverla precisamente por cartesianas pues aun no hemos visto cilíndricas ni esféricas ni el teoremas de cambio de variable, asi que toca por cartesianas.
No tengo muy buen programa para tres dimensiones, esta es la gráfica.
Para una altura h el volumen será la integral entre 0 y h de las áreas de los círculos que se cortan horizontalmente. El radio del círculo que esta a altura h es tal que
x^2 + y^2 = h
midiéndolo por donde y=0 será
x^2 = h
x = sqrt(h)
Luego el área del círculo a altura h es pi·[sqrt(h)]^2 = pi·h
Y la integral de todas estas áreas es
$$\int_0^h \pi h dz = \pi hz|_0^h= \pi h^2$$
Y así es como se puede calcular, con la integral que propónías tu era muy difícil.
Y eso es todo.
valeroasm la expresión que pones arriba: x^2 + y^2 = h, no seria con h^2 ?
y porque mides el circulo por donde y=0 ? pudiste haberlo hecho haciendo x=0 también? con que fin haces eso, con el fin de cancelar las integrales respecto de x e y ?
el resultado entonces daría lo mismo con la integral que tu planteas?
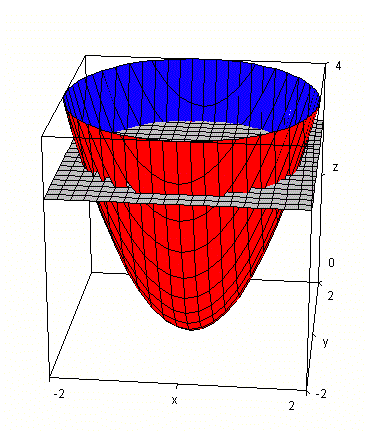
Vamos a ver que no lo hice muy bien. No leí el último cuadrado que habías escrito a mano, otra vez ponlo como expresión matemática, es mucho más comodo leer
x^2 + y^2 = z^2
La gráfica cambia un poco pero el método será igual.
El volumen es la integral de las superficies de los círculos que se obtienen al cortar horizontalmente. Necesitamos conocer el radio de cada círculo dependiendo de la altura
La circunferencia intersección a una altura zo tiene por ecuación
z = zo ==> z^2 = zo^2
z^2 = x^2 + y^2
x^2 + y^2 = zo^2
Esta es la ecuación de una circunferencia de radio zo.
Por lo tanto el área del círculoi será
A(zo) = pi·zo^2
Puesto como función de z es
A(z) = pi·z^2
Y el volumen es la integral de estas áreas a lo largo del eje z desde el vértice donde z=0 hasta h.
$$\int_0^h \pi z^2 dz = \left.\pi \frac{z^3}{3}\right|_0^h= \pi \frac{h^3}{3}$$Lo cual es verdadero ya que se trata del volumen de un cono
V = (1/3)pi·r^2·h
y como este cono tiene igual radio que altura
V = (1/3)pi·h^3
No he conseguido programa que logre resolver tu integral para comprobarla. Se supone que tiene que dar ese mismo resultado, pero los diferenciales de volumen que has tomado para integrar no son los más apropiados.
Y eso es todo.
