Vamos ha hacer el dibujo para entenderlo.
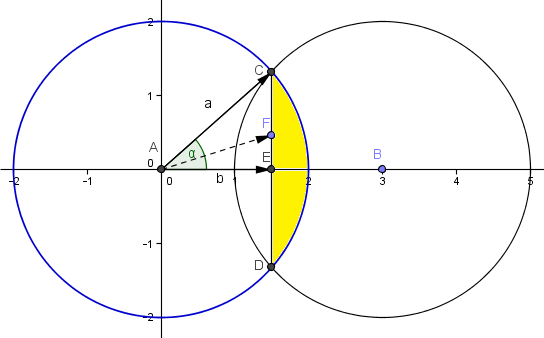
Falta la perspectiva tridimensional pero puede entenderse. Debemos hallar el volumen del casquete en amarillo, multiplicado por dos será el volumen que nos piden.
SI QUIERES salta hasta donde dice "NADA, esto no hay quien lo integre"
Vamos a calcular los límites en coordenadas esféricas.
Verticalmente el ángulo de barrido será fi = [pi/2 - alfa, pi/2 + alfa]
y horizontalmente es theta € [-alfa, alfa] donde:
$$\alpha=arctg\left(\frac{\sqrt{a^2-b^2}}{b} \right)$$Bueno, puede que en tu libro cambien el fi con el theta o el fi lo pongan como ángulo de elevación en vez de declive, pero son cosas inevitables.
Los límites del radio vector son un poco más complicados de hallar.
El limite superior es a, eso no ofrece dudas, pero el inferior hay que calcularlo.
La proyección en el plano que se ve en el dibujo del radio vector es:
Sea beta el ángulo EAF, entonces
AF = b/cos(beta)
como beta = pi/2 -fi
AF = b / cos(pi/2-fI) =
b / [cos(pi/2)cos(fi)+sen(pi/2)sen(fi)] =
b / sen(fi)
AF = b / sen(fi)
Y la proyección del radio vector en el plano z=0 es mas sencilla porque el angulo gamma que pongamos equivalente al beta anterior coincide con el theta
proyección en plano horizontal = b/cos(theta)
Y el modulo del radio vector es el módulo de la suma de los dos
$$\rho(\theta,\varphi)=b \sqrt{\frac{1}{\cos \theta}+ \frac{1}{sen \varphi}}$$Entonces los límites de integración de ro son entre eso que hemos puesto y a.
Y en la teoría debes tener que el jacobiano del cambio de variables a esféricas es
J=ro^2·sen(fi)
Entonces el volumen de ese casquete esférico es
$$\begin{align}&V=\int_{-\alpha}^{\alpha}\int_{\frac{\pi}{2}-\alpha}^{\frac{\pi}{2}+\alpha}\int_{b \sqrt{\frac{1}{sen\varphi}+\frac{1}{\cos\theta}}}^{a} \rho^2sen\varphi\;d\rho\;d\varphi\;d\theta=\\ &\\ &\end{align}$$NADA, eso no hay quien lo integre.
El enunciado no dice nada de tenga que ser una integral multiple, vamos a hacerlo con una integral simple que es lo que pensaba desde el principio. Además lo que vamos a hacer tiene implícita una integral doble para calcular el área del cículo, luegon puede considerarse como triple
Vamos a tomar como elementos diferenciales las rodjas que se obtienen al cortar en vertical, las cuales son circunferencias y su área es pi·z^2
Donde z es el radio de las rodajas que cada una tiene un radio distinto. La integral de la areas de todas las rodajas de la zona amarilla da su volumen.
La integación será a traves del eje X entre b y a
El radio (es decir la altura de la rodaja) en un punto x será
z=sqrt(a^2-x^2)
por lo tanto el área de la rodaja será
A=pi(a^2-x^2)
y el volumen es la integral
$$\begin{align}&V=\int_b^a \pi(a^2-x^2)dx=\\ &\\ &\pi\left[a^2x-\frac{x^3}{3} \right]_b^a=\\ &\\ &\pi\left(a^3-\frac{a^3}{3}-a^2b+\frac{b^3}{3}\right)=\\ &\\ &\frac{\pi}{3}(3a^3-a^3-3a^2b+b^3)=\\ &\\ &\frac{\pi}{3}(2a^3-3a^2b+b^3)\\ &\\ &\text{No olvidar que esto era la mitad del volumen que dicen}\\ &\\ &V_{total}=\frac{2\pi}{3}(2a^3-3a^2b+b^3)\end{align}$$Y en el ejercicio nos dan una expresión distinta por usar d, vamos a ver que son lo mismo. Solo queda demostrar que
$$\begin{align}&d^2(3a-d)=2a^3-3a^2b+b^3\\ &siendo\; d=a-b\\ &\\ &(a-b)^2(3a-(a-b))=\\ &\\ &(a^2+b^2-2ab)(2a+b)=\\ &\\ &2a^3+a^2b+2ab^2+b^3-4a^2b-2ab^2=\\ &\\ &2a^3-3a^2b+b^3\end{align}$$Exacto, justo lo que piden.
Pensaba que podría hacerse con coordenadas esféricas y no se puede, así que olvídate de todo lo que hice al principio, pero es que no podía borrarlo con todo lo que tuve que pensar y lo que me costó, por eso lo he dejado.


