Pedro no se si lo que quieres es saber la respuesta o el procedimiento para resolverlo de todas formas hago el desarrollo a continuación y al final está la respuesta. Te aconsejo que en tus preguntas siempre expliques el contexto del problema por ejemplo no se que nivel de estudios tienes ni para que quieres resolverlo esto ayuda mucho generalmente.
Para resolverlo utilicé la siguiente codificación:
Fe=flujo de entrada=10 Fs=flujo de salida=15
M=masa del tanque=variable dependiente
M0=masa en el tanque a tiempo cero=100
t= tiempo=variable independiente=10 (únicamente al final toma este valor)
xe=concentracion de sal a la entrada=0,10
xs=concentraciónde sal en la salida=variable dependiente
x=concentracion de sal en el tanque=variable dependiente
x0=concentracion de sal dentro del tanque a tiempo 0=0,6
Las ecuaciones son las siguientes:
Tenemos 2 ecuaciones
1)Fe-Fs=dM/dt la masa acumulada en el tanque con el tiempo es la diferencia entre los flujos de entrada y salid (balance de masa total)
2)Fe*xe-Fs*xs=d(M*xt)/dt la masa DE SAL acumulada en el tanque con el tiempo es la diferencia entre la SAL que entra y la que sale (balance para el componente sal)
Para poder resolver tenemos que hacer la simplificación de que la concentración dentro del tanque es igual a la que se extrae del tanque esto equivaldría a un tanque de mezcla perfecta en el que lo que se saca es lo mismo que lo que esta adentro o Homogéneo (xs=x)
La segunda ecuación contiene la derivada de un producto por lo que la desarrollaremos:
3) Fe*xe-Fs*x=(dM/dt)*x+(dxt/dt)*M
El termino dM/dt es reemplazado por Fe-Fs (por la ecuación 1)
El termino M es reemplazado por (Fe-Fs)*t+M0 (resolviendo ecuación 1, ecuación diferencial a variables separadas)
Reemplazando, en la ecuación 3 nos queda:
Fe*xe-Fs*x=(Fe-Fs)*x+dx/dt*((Fe-Fs)*t+M0)
dividiendo todo por (Fe-Fs) y como (Fs/Fe-Fs)*x+x=fe*x nos queda
dx/dt*(t-M0/(Fe-Fs))+Fe*x=Fe*xe/(Fe-Fs)
dividiendo todo por (t-M0/(Fe-Fs))
dx/dt+Fe/(t-M0/(Fe-Fs))*x=Fe*xe/(Fe-Fs)/(t-M0/(Fe-Fs))
que parece una ecuación bastante fea pero reemplazando todos los valores nos queda
dx/dt+10/(t+20)*x=-5/(t+20)
Que tiene la forma de una ecuación diferencial lineal de primer orden como la siguiente
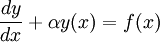
cuya solución es la siguiente:
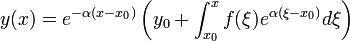
en nuestro caso
alfa=10/(t+20)
f=-5/(t+20)
ten cuidado de no confundirte con la imagen porque en nuestro caso y es x y x es t
Esta parte es bastante dificil, si no sabes bien matemática, podes resolverlo con algún programa de computadora o con método numéricos(aproximados) la cuestión es que la solución para t=10 nos queda
x=0,391
bueno ahora vamos a responder a la pregunta cual es la cantidad de sal?
bueno la cantidad de sal es la concentración x multiplicada por la cantidad total del tanque que para 10 minutos por ecuación 1 es M=(Fe-Fs)*t+M0=50
o sea que 0,391*50=19,55
La respuesta es 19,55 kg de sal luego de 10 min

