Sumas de Riemann (3) f(x) = x - 5 en el intervalo (2,5)

Te haré la suma superior de Riemman, para n subintervalos,

f(x)=x-5

$$\begin{align}&Ancho  \ de \ cada \ subintevalo:\\&\Delta x=\frac{b-a}{n}= \frac{5-2}{n}= \frac{3}{n}\\&\\&abscisa \ del\ extremo \ derecho \ de \ cada \ subintervalo:\\&x_i=a+i \Delta x\\&i \ indicaría \ el \ número \ de \ cada \ subintervalo \ de \ izquierda \ a \ derecha\\&\\&x_i=2+i \frac{3}{n}\\&\\&La \ n-ésima \ Suma \ de \ Riemann:\\&\sum_{i=1}^{n}f(x_i)·\Delta x=\sum_{i=1}^{n}f(2+\frac{3i}{n})·\frac{3}{n}=\sum_{i=1}^{n}(2+\frac{3i}{n}-5)\frac{3}{n}=\\&\\&\sum_{i=1}^{n} (\frac{3i}{n}-3)\frac{3}{n}= Las \ constantes \ salen \ fuera \ del \ sumatorio\\&\\&\frac{3}{n}\sum_{i=1}^{n}(\frac{3i}{n}-3)=\frac{3}{n}(\sum_{i=1}^{n}\frac{3i}{n}-\sum_{i=1}^{n}3)=\\&\\&\frac{3}{n} \left( \frac{3}{n}\sum_{i=1}^{n}i-\sum_{i=1}^{n}3  \right)=**\\&\\&propiedades \ sumatorios:\\&\sum_{i=1}^{n}k=kn\\&\sum_{i=1}^{n}i=\frac{n(n+1)}{2}\\&\\&**= \frac{3}{n} \left( \frac{3}{n}·\frac{n(n+1)}{2}-3n \right)=\\&\\&\frac{3}{n} \left( \frac{3(n+1)}{2}-3n \right)=\\&\\&\frac{3}{n} \left( \frac{3n+3}{2}-3n \right)= \frac{3}{n} \left( \frac{3n+3-6n}{2} \right)=\\&\\&\frac{3}{n} \left( \frac{3-3n}{2} \right)=\frac{9-9n}{2n}\\&\\&Suma \ Riemann\\&\lim_{n \to \infty}  \frac{9-9n}{2n}= \frac{-9}{2}\\&\\&\\&\\&\\&\\&\end{align}$$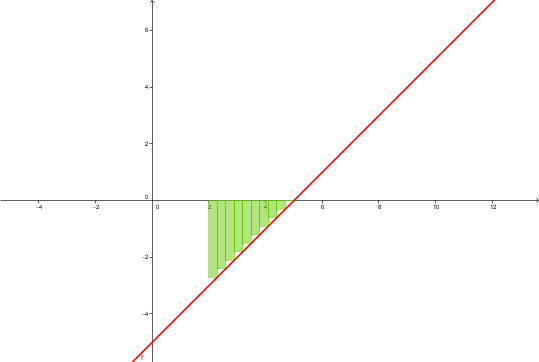

La suma da negativa, porque la función es negativa en (2,5)

Elige más temas para las preguntas:

Matematicas, calculo, ingenierias...

Saludos Lucas mmm, gracias por resolver el ejercicio, hay otros 2 ejercicios que puse sobre sumas de riemann, espero puedas ayudarme... . tengo una duda sobre la gráfica, no se supone que debe hacer curva, ¿digo por lo que he visto de los ejercicios de este tipo siempre se generan curvas no es así?

No te preocupes por tu calificación voy a poner excelente, siempre lo hago