Graficar y analizar las siguientes funciones
a) f(x) = ¨{x - 2}
b) f(x) = 1/x+3
c) f(x) = (x+4)al cuadrado
d) f (x) = e a la x-1
1 respuesta
No se entiende cuál es la primera función, las llaves no tienen significado.
La segunda no se sabe si es
(1/x)+3
o
1/(x+3)
La cuarta tampoco sé si es
e^(x) + 1
o
e^(x+1)
No sé hasta que punto llega el análisis, eso depende del curso que estés realizando. Dime que elementos hay que analizar de estos:
Dominio
Continuidad
Imagen
Periodo
Cortes con el ejes
Asíntotas
Máximos-mínimos, puntos de inflexión
Intervalos de crecimiento-decrecimiento
Intervalos de concavidad-convexidad
O algún otro que me haya olvidado.
Dime únicamente los que te piden, ya es suficiente que sean 4 ejercicios para hacer encima cosa que no piden.
a) f(x) = x-2
b) f(x) = 1/x+3 1 dividido sobre x + 3
c) f(x) = (x + 4)^2
d) f(x) = e^x-1
colaborarme con estos ejercicios.. que te lo agradezco..
Insisto. No aclaras nada las dudas que te planteé, te has limitado ha volver a copiar lo mismo. Tienes que aprender a usar los paréntesis para evitar las ambigüedades. Tú estas viendo la función escrita en el libro pero yo no, soy ciego y tienes que describírmela perfectamente para que sepa cuál es.
Cuando tu escribes una / yo no sé cuándo termina, si en el siguiente término o al final o por el medio. Ahora bien, si después de la barra pones el denominador entre paréntesis, yo sabre dónde termina la barra
Es por eso que:
1/x+3 no me dice nada porque puede ser estas dos cosas
$$\begin{align}&\text{(1/x)+3} =\frac{1}{x}+3\\ &\\ &\\ &\\ &o\\ &\\ &\\ &\text{1/(x+3)} = \frac{1}{x+3}\end{align}$$Dime si es la uno o la dos. De acuerdo con las normas de prelación de operaciones sería la uno, pero me temo que tú quieres decir la dos. Especifica.
Y tres cuartas partes de lo mismo pasa con
e^x-1
Que puede significar
$$\begin{align}&\text{(e^x)-1} = e^x-1\\ &\\ &\\ &\text{o}\\ &\\ &\text{e^(x-1)} = e^{x-1}\end{align}$$De nuevo la opción que se adecua a lo que escribiste es la uno, pero confírmame si es la uno o la dos.
Y respecto al análisis dime cuáles de las cosas que te dije te piden. No es lo mismo el análisis para una edad de 14 años que de 17. Si hay cosas que no te suenan no te las van a pedir.
Por favor, hay que concretar bien las preguntas.
hola , un saludo
mira en ambos ejercicios es la opción 2 que tu planteas.... en cuanto al análisis es el dominio, continuidad, periodo y cortes en el eje....
te agradezco la ayuda...
Estas son las gráficas de las funciones. Creo que se distinguen bastante bien.
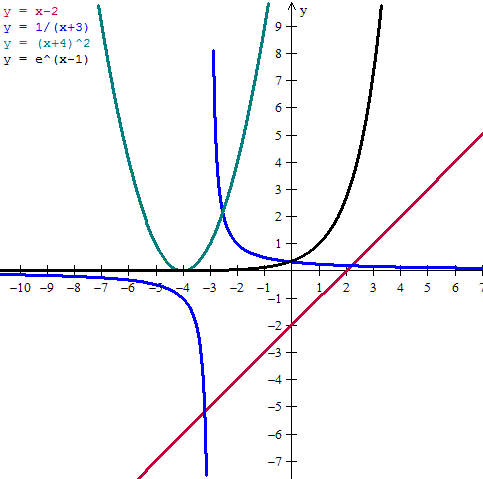
a) f(x) = x-2
Es una recta.
El dominio es todos los números reales. Dom f = R
Es continua en todo R.
No es periódica
Los cortes con los ejes son:
Cortes con el eje X. Suceden cuando y = 0
0 = x -2
-x=-2
x=2
Es el punto (2,0)
Cortes con el eje Y. Suceden cuando x = 0
y = 0-2
y = -2
Es el punto (0,-2)
b) f(x) = 1/(x-3)
Una función racional (cociente de polinomios) no está definida cuando el denominador es cero
x-3 = 0
x = 3
Luego Dom f = R - {3}
Es continua en todo su dominio, ya que el punto x=3 no pertenece al dominio.
No es periódica.
No tiene cortes con los ejes, es siempre positiva o negativa, en el +-infinito es cuando tiende a cero.
Tiene asíntota vertical, la recta x=-3
y asíntota horizontal la recta y=0
c) f(x) = (x+4)^2
Es una parábola.
Su dominio es todo R. Dom f = R
Es continua en todo su dominio.
No es periódica.
Los cortes con el eje X son cuando y = 0
0=(x+4)^2
0=x+4
x=-4
el punto (-4,0)
El corte con el eje Y es cuando x = 0
y = (0+4)^2
y = 4^2 = 16
Es el punto (0,16)
d) f(x) = e^(x+1)
Es una función exponencial.
Su dominio es todo R. Dom f = R
Es continua en todo su dominio.
No es periódica.
No tiene cortes con los ejes, es siempre positiva. En -infinito es cuando tendería a cero
Tiene asíntota horizontal, es la recta y=0
Y eso es todo. Espero que te sirva y lo hayas entendido. Si hace falta algo más dímelo.
