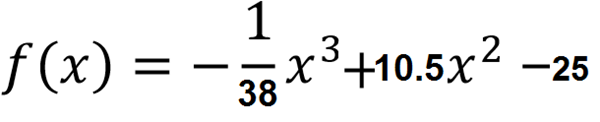¿Determina los intervalos de crecimiento y de decrecimiento de la función así como los de concavidad para la siguiente función?
Considera la función
Determina lo siguiente:
- La derivada de la función, lo más simplificada posible.
- Los valores críticos de la función.
- Si los valores críticos son máximos o mínimos. Para ver cuál es máximo y cual mínimo calculamos la derivada segunda.
- Los intervalos de crecimiento y de decrecimiento de la función así como los de concavidad
·
1) La derivada es:
$$\begin{align}&f'(x) = \frac{3}{38}x^2+21x\\&\\&\text{2)}\\&\text{los puntos críticos son los que hacen f'(x)=0}\\&\\&\frac{3}{38}x^2+21x=0\\&\\&\left(\frac{3}{38}x+21\right)x = 0\\&\\&x_1=0\\&\\&\frac{3}{38}x + 21=0\\&\\&\frac 3{38}x=-21\\&\\&x=-\frac{21·38}{3}=-7·38 =- 266\\&\\&x_2=-266\end{align}$$Luego hay dos puntos críticos
{-266, 0}
·
3)
Calculamos la derivada segunda para saber si son máximos o mínimos.
f''(x) = (6/38)x + 21
f(-266) = (6/38)(-266) + 21 = -1596/38 + 21 = -42+21 = -21
Por ser negativa la derivada segunda hay un máximo en x=-266
f(0) = 21
Por ser posítiva la derivada segunda hay un mínimo en x=0
4) Los puntos críticos delimitan los cambio de signo de la derivada primera. Luego tenemos tres intervalos:
f '(x) = (3/38)x^2+ 21x
Es un polinomio de grado 2 con coeficiente positivo para x^2, luego es una parábola con forma de U, tiende a +infinito tanto por la izquierda como por la derecha y entre medio de las dos raíces es negativa. Luego:
(-Infinito, -266) derivada primera positiva luego f es creciente
(-266, 0) derivada primera negativa, luego f es decreciente
(0, +infinito) derivada primera positiva luego f es creciente.
·
Los intervalos de concavidad están delimitados por las raíces de la derivada segunda
f''(x) = (6/38)x + 21 = 0
(6/38)x = -21
x = -21·38 / 6 = -7 · 19 = -133
f''(x) es una recta con pendiente positiva, luego a la izquierda de la raíz tendra valores negativos y a la derecha positivos, entonces
(-Infinito, -133) la derivada segunda es negativa, luego f es cóncava hacia abajo
(-133, +infinito) la derivada segunda es positiva, luego f es cóncava hacia arriba
·
Cuando yo estudiaba en el colegio cóncava era forma de U y convexa al revés. Luego en la universidad, tal vez influido porque el profesor habia hecho un curso especial en EEUU la que tenía forma de U era la convexa. Así que para evitar líos uso la nomenclatura cáncava hacia arriba y cóncava hacia abajo que he visto en algunos sitios.
Cóncava hacia arriba significa forma de U y cóncava hacia abajo significa forma de iglú.
·
Y eso es todo.
