Gràfica de la funciòn sqrt(x^2 + 2x - 2)

·

Deberías dar más detalles.

Dices que tabla de valores no

Dime cuáles de estos deben calcularse.

1) Dominio

2) Rango

3) Cortes con los ejes

4) Máximos y mínimos

5) Perioodos de crecimiento y decreciemiento

6) Concavidad

...

Bueno, dominio y rango dices que sí.

El dominio de una función raíz cuadrada son aquellos valores de x donde el interior de la raíz es positivo

x^2 + 2x - 2 >= 0

Esta es la típica gráfica de una parábola con forma de U. Entonces es positiva a los lados de las raíces y negativa entre ellas. Calculemos las raíces.

$$\begin{align}&x=\frac{-2\pm \sqrt{4+8}}{2}=\\&\\&\frac{-2\pm 2 \sqrt 3}{2}= -1\pm \sqrt 3\\&\\&\text{Luego el dominio es}\\&\\&Dom f=(-\infty, -1-\sqrt 3]\cup[-1+\sqrt 3, +\infty)\end{align}$$

El rango es [0, +infinito)

Ya que por ser una raíz cuadrada será siempre mayor que 0, y sabemos que hay dos puntos donde lo vale. Y es una función que tiende a infinito cuando x tiende a -infinito o + infinito y es continua, lueggop toma todos los valores entre 0 y +infinito

Los puntos de corte con el eje X ya están calculados, son los que limitan el dominio, veanse. Si acaso los voy a poner aquí en decimal para que los puedas dibujar

(-2.732, 0)  y (0.732, 0)

Con el eje Y no hay cortes ya que en x=0 no está definida la función.

No hay puntos que anulen la derivada

$$\begin{align}&f(x) = \sqrt{x^2+2x-2}\\&\\&f'(x) = \frac{2x+2}{2 \sqrt{x^2+2x-2}}=\\&\\& \frac{x+1}{\sqrt{x^2+2x-2}}= 0\\&\\&x+1 = 0\\&\\&x=-1\end{align}$$

Pero en -1 no está definida la función, no esta definida en el intervalo

(-2.732, 0.732)

Por lo tanto no hay máximos ni mínimos

En el intervalo (-infinito, -2.732] el valor del numerador de la derivada

x+1 es siempre negativo, luego la función es decreciente

Y en el intervalo (0.732, +infinito) ese valor es siempore positivo, luego la función es creciente.

La derivada segunda es:

$$\begin{align}&f'(x) = \frac{x+1}{\sqrt{x^2+2x-2}}\\&\\&f''(x) = \frac{\sqrt{x^2+2x-2}-(x+1)·\frac{x+1}{\sqrt{x^2+2x-2}}}{x^2+2x-2}=\\&\\&\frac{x^2+2x-2-(x+1)^2}{(x^2+2x-2)\sqrt{x^2+2x-2}}=\\&\\&\frac{-4}{(x^2+2x-2)\sqrt{x^2+2x-2}}\end{align}$$

como (x^2+2x-2) tiene que ser positivo, entonces el deniominador es siempre positivo y la derivada segunda es siempre negativa.  Luego la función es cóncava hacia abajo como un iglú.

Y eso es todo se sabe donde empieza, a donde llega y como llega. No estará mal de todas formas calcular algún punto para hacerla mejor.

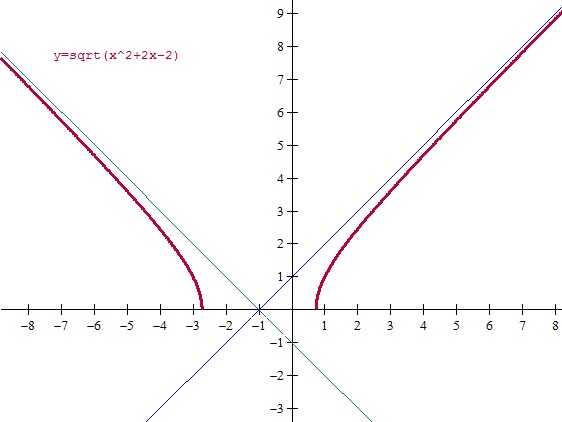
Al hacer la gráfica me he dado cuenta de un detalle que se me paso por alto. La gráfica tiene asíntotas verticales ya que

Espera un poco, que se mandó sola la respuesta.