Diosa Lara!
·
No puedo dibujar figuras en tres dimensiones. Pero hay problemas que se pueden solucionar sin ello. En este calculas el dominio en el plano XY y luego sobre ese dominio se integra la función z.
El dominio en el plan xy te lo dan las funciones
x=Y es la típica línea diagonal que pasa por el origen y corta el primer y tercer cuadrante.
La función x=y^2 es la parábola tumbada, tiene forma de C.
La superficie comprendida entre las dos funciones es como un gajo de naranja (más o menos).
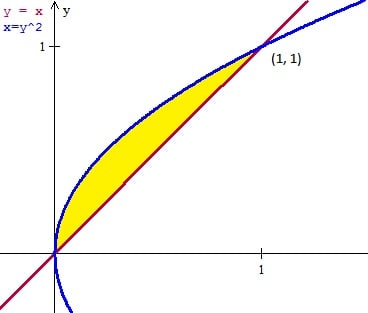
Y el dominio será
x entre 0 y 1
Y para calcular el dominio en y tenemos que tener las dos funciones en funcion de x
y=x
y=sqrt(x)
Luego los límites en y son x y sqrt(x)
Y para los límites en z debemos despejar la función z
x+z^2=1
z = sqrt(1-x)
Como nos dicen en el primer octante es la parte superior del plano z=0, luego los límites en z son 0 y sqrt(1-x)
Los límites en z no suelen ponerse siempre, ya directamente se pone la función superior menos la inferior y la integral es doble en vez de triple
$$\begin{align}&V=\int_0^1\int_x^{\sqrt x}\sqrt{1-x}\;dy\,dx=\\&\\&\int_0^1 \sqrt{1-x}\int_x^{\sqrt x}dydx=\\&\\&\int_0^1 \sqrt{1-x}·y|_x^{\sqrt x}dx=\\&\\&\int_0^1 \sqrt{1-x}(\sqrt x-x)dx\end{align}$$Yo diría que se han pasado un poco con esta integral. Intenta terminarla y si no puedes ya me lo dirás, pero lleva su tiempo.

