Calcular el volumen en 3 dimensiones

Diosa Lara!

·

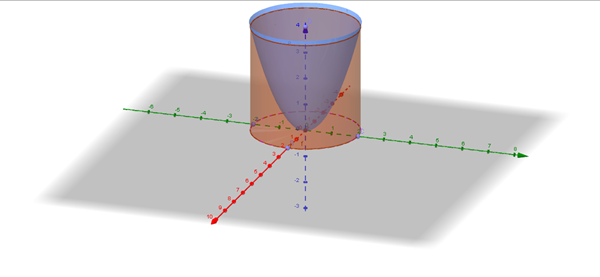
Has hecho muy bien el dibujo.

Nos dicen el primer octante. Eso hace que las 3 variables sean positivas y el 0 será el límite inferior de las tres variables de integración, ya que no no hay otro límite inferior mayor por otras condiciones o por la posición d las superficies.

Como el cilindro tiene radio 2 en el eje x tomaremos límites [0,  2]

En el eje Y tomaremos [0 , sqrt(4-x^2)]

Y en el eje Z tomaremos [0, z(x,y)] = [0, x^2+y^2]

$$\begin{align}&\int_0^2\int_0^{\sqrt{4-x^2}}(x^2+y^2)dydx=\\&\\&\int_0^2\left[x^2y+\frac{y^3}{3}  \right]_0^{\sqrt{4-x^2}}dx=\\&\\&\int_0^2\left(x^2 \sqrt{4-x^2}+\frac{\sqrt{(4-x^2)^3}}{3}\right)dx\end{align}$$

Bueno, tal vez sean un poco difíciles aunque se puedan hacer.

Vamos a hacerlo en coordenadas cilíndricas.

El primer cuadrante se recorre con un radio-vector con longitud (rho) entre 0 y 2 y un ángulo (theta) entre 0 y pi/2.

La función z corresponde en cada punto con el radio-vector elevado al cuadrado

Ya que

rho=sqrt(x^2+y^2)

Y el jacobiano de la transformación es rho.

Luego la integral será:

$$\begin{align}&\int_0^2\int_0^{\pi/2}\int_0^{\rho^2}\rho\; dz\,d\theta\,d\rho=\\&\\&\int_0^2\int_0^{\pi/2} \rho\, z|_0^{\rho^2}\; d\theta\,d\rho=\\&\\&\int_0^2\int_0^{\pi/2}\rho^3  d\theta\,d\rho=\\&\\&\int_0^2\rho^3\theta|_0^{\pi/2}d\rho=\\&\\&\int_0^2\rho^3·\frac \pi 2\;d\rho=\\&\\&\left.\frac \pi 2·\frac{\rho^4}{4}\right|_0^2=2\pi\end{align}$$

Y como yo no acabo de fiarme de estos cambios lo que haré es meter la integral en cartesianas en el ordenador para comprobar si está bien.  Y también da 2pi, luego está bien.

Y eso es todo.