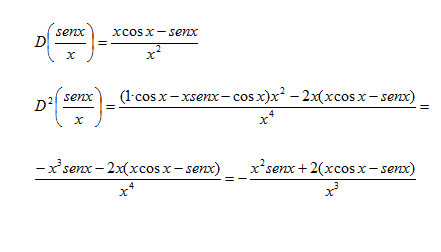¿Calcular f'(0) y f''(x) dada la siguiente funcion f(x)?
¿Hola qué tal me podrían ayudar con esta función?
2 Respuestas
·
Voy a hacer algo distinto de lo que ya tienes.
$$\begin{align}&f'(0)=\lim_{h\to0}\frac{f(0+h)-f(0)}{h}=\\&\\&\\&\lim_{h\to 0}\frac{\frac {senh}h-1}{h}=\lim_{h\to 0}\frac{senh-h}{h^2}=\\&\\&\text{el desarrollo de Taylor de la función seno es}\\&\\&sen h=h-\frac{h^3}{3!}+ o(h^5)\\&\\&=\lim_{h\to 0}\frac{h-\frac{h^3}{3!}+ o(h^5)-h}{h^2}=\\&\\&=\lim_{h\to 0}\frac{\frac{h^3}{3!}+ o(h^5)}{h^2}=\\&\\&\frac{h}{3!}+o(h^3)=0+0=0\end{align}$$Yo creo que también habria que calcular la derivada segunda en el 0 ya que la función esta indefinida en ella.
Dado que la derivada primera es
$$\begin{align}&f'(x)=\frac{x\,cosx-senx}{x^2}\quad \text{ si x}\neq 0\\&\\&f'(0) = 0 \\&\\&tendremos\\&\\&f''(0) = \lim_{h \to 0}\frac{\frac{h\,cosh-senh}{h^2}-0}{h}=\\&\\&\lim_{h\to 0}\frac{h\,\cos h-senh}{h^3}=\\&\\&\text{Como}\quad senh=h-\frac{h^3}{3!}+o(h^5)\\&\text{Y como }\quad cosh=1-\frac{h^2}{2!}+o_2(h^4)\\&\\&=\lim_{h\to 0}\frac{h-\frac{h^3}{2!}+o_2(h^5)-h+\frac{h^3}{3!}-o(h^5)}{h^3}=\\&\\&\lim_{h\to 0}\frac{h^3\left(-\frac 12+\frac 16\right)+o_3(h^5)}{h^3}=\\&\\&-\frac 13+o_3(h^2) =-\frac 13\\&\end{align}$$Los o(h^n) se llaman infinitésimos de orden n no se si los habrás estudiado. Son funciones que tienden a 0 pero de forma más rápida que h.
Y eso es todo.
¡Ah por cierto! Puede parecer en la gráfica que la derivada segunda sea -1 ya que la tangente parece una diagonal de 45º. Pero esa gráfica esta desproporcionada completamente, las medidas en el eje Y son mucho más grandes que en el X.
La derivada de la fracción es
Que sirve para x distintos de 0
f'(0)=0 siempre y cuando el límite siguiente valga 0
$$\begin{align}&\lim_{x \to 0} \frac{xcosx-senx}{x^2}=\frac{0}{0}=Regla\ L'Hopital=\\&\\&\lim_{x \to 0}\frac{1cosx-xsenx-cosx}{2x}=\lim_{x \to 0}\frac{senx}{2}=0\\&\\&\end{align}$$Luego
$$\begin{align}&f'(0^-)=f'(0^+)=f'(0)=0\end{align}$$Te adjunto las gráficas de f= senx/x y f' donde se observa que la función es derivable en 0 y vale cero la derivada
