Ejercicios de gráficas y funciones

Ya contesté esta pregunta, pero por si acaso voy a dar una respuesta distinta a la primera

1. Traza la gráfica de la siguiente función exponencial
f(x) = 4x

Tal como la tienes escrito eso es 4 por x. Si fuera una función exponencial sería 4 elevado a la x, y eso se escribiría así:

f(x) = 4^x

Sobre esta función podemos decir calcular los límites en -infinito y + infinito

$$\begin{align}&\lim_{x\to -\infty}4^x = \frac{1}{4^{\infty}}=0\\ &\\ &\\ &\lim_{x\to \infty}4^x= 4^{\infty}=\infty\end{align}$$

De otra parte es siempre positiva, luego no corta al eje X. Y el corte con el eje Y es

(0, 4^0) = (0, 1)

Y la función es siempre creciente porque la derivada es

f '(x) = 4^x · ln 4

Que es siempre positiva

Y la derivada segunda es

F ''(x) = 4^x ·(ln 4)^2 que también es siempre positiva, luego es cóncava hacia arriba.

Y con eso y algún punto más como por ejemplo

(1,4), (2,16), (-1, 1/4), (-2, 1/16)

podemos hacer la gráfica.

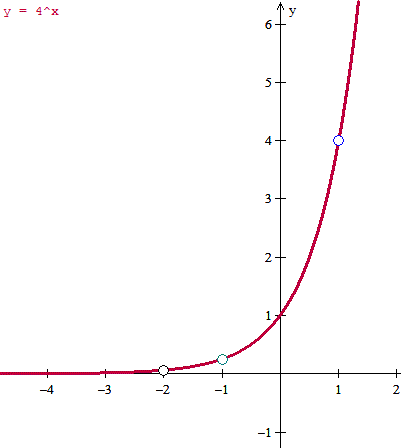
Y las otras dos partes ya estaban respondidas.