Calculo diferencial:Derivación de orden superior e implícita
debo de determinar la derivada de las funciones implícitas y de orden superior, pero no entiendo el material proporcionado, además de realizar las demostraciones funciones.
Calcular la derivada de orden superior:
d^3/(dx^3) (x^5 e^3x)
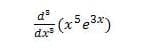
1 respuesta
Respuesta de Valero Angel Serrano Mercadal
1
·
Bueno, ya viste que no es más que derivar tres veces, nos vamos a dejar de tanta notación y explicaciones como en la vez anterior. Llamemos f(x) a la función.
$$\begin{align}&f(x) =x^5e^{3x}\\&\\&f'(x) = 5x^4e^{3x}+x^5·e^{3x}·3=(5x^4+3x^5)e^{3x}\\&\\&\\&f''(x)=(20x^3+15x^4)e^{3x}+(5x^4+3x^5)e^{3x}·3 =\\&\\&(20x^3+30x^4+9x^5)e^{3x}\\&\\&\\&f'''(x) = (60x^2+120x^3+45x^4)e^{3x}+(20x^3+30x^4+9x^5)e^{3x}·3=\\&\\&(60x^2+180x^3+135x^4+27x^5)e^{3x}\end{align}$$Y eso es todo.
