Demostrar paso a paso el siguiente enunciado:

Para demostrar esto he utilizado:

El Teorema del coseno y

La Fórmula Trigonométrica del Área de un Triángulo (calcula el área en función de dos lados cualesquiera y el ángulo comprendido)

Supongo las conoces, sino son fáciles de encontrar la demostración en la web.

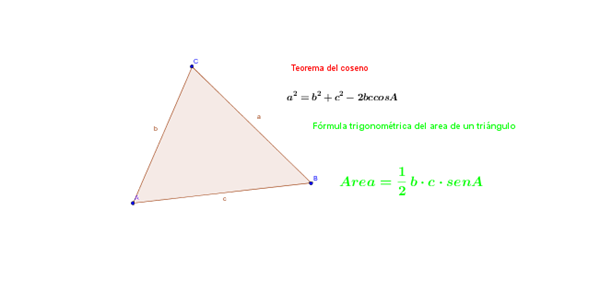
El triángulo que muestras es rectángulo e isósceles (tiene dos ángulos de 45º)

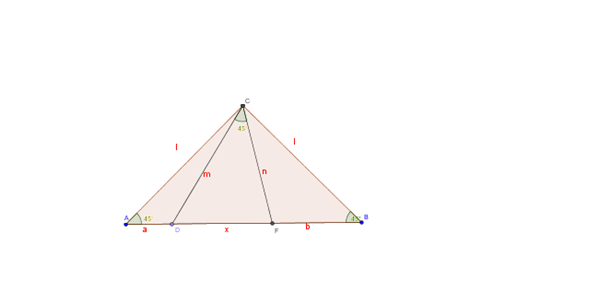
Los lados iguales, miden l

y las cevianas miden m y n

Aplicando el Teorema del coseno en los triángulos CDF (para x)

ADC (para m) y CFB para n tenemos:

$$\begin{align}&\Delta CDF\\&x^2=m^2+n^2-2mn·cos45\\&x^2=m^2+n^2-2mn·\frac{\sqrt 2}{2}\\&x^2=m^2+n^2- mn \sqrt 2\\&\\&\Delta ADC:\\&m^2=a^2+l^2-al \sqrt 2\\&\\&\Delta CFB:\\&n^2=b^2+l^2-bl \sqrt 2\\&\\&Sustituyendo \ las \ dos \ últimas \ en \ la \ primera:\\&x^2=a^2+l^2-al \sqrt 2+b^2+l^2-bl \sqrt 2-mn \sqrt 2\\&x^2=(a^2+b^2)+(2l^2-al \sqrt 2 - bl \sqrt 2 - mn \sqrt 2)\\&Como \ queremos \ demostrar \ que \  x^2=a^2+b^2\\&hay  \ que \ demostrar \ que \ el \ segundo \ paréntesis \ es \ cero.\\&\\&Estratégia \ del \ Area:\\&[ABC] \ quiere \ decir \ Area \ del \ triángulo \ ABC\\&[ABC]=\frac{1}{2}l·l=\frac{1}{2}l^2  \ (es  \ un \ triángulo \ rectángulo)\\&[ADC]+[CDF]+[FCB]=\\&\frac{1}{2}al·sen45+\frac{1}{2}mnsen45+\frac{1}{2}bl·sen45=\\&\frac{1}{2}·\frac{\sqrt 2}{2}(al+mn+bl)\\&\\&\\&Igualando \las \ Areas:\\&\frac{1}{2}·\frac{\sqrt 2}{2}(al+mn+bl)=\frac{1}{2}l^2\\&\\&\Rightarrow\\&\sqrt 2 (al+mn+bl)=2l^2\\&Luego \ el \ segundo \ paréntesis \ es \ cero\\&cumpliéndose\\&x^2=a^2+b^2\\&\end{align}$$

Espero que te sirva

Recuerda Votar.

Votar Excelente es lo correcto y más en un problemita como este.

Un placer.

Gracias! Solo una pequeña duda por que el sehundomparentesis en la parte final vale 0 ?

·

¿Pero seguro que deben ser esos los ángulos? Si los ángulos son de 45º tendremos que el triángulo derecho no existirá, con lo cual b=0.

Y x=a porque son dos triángulos iguales por tener los mismos ángulos y un lado común.

y de x=a tenemos

x^2 = a^2

y como b=0

x^2 = a^2 + b^2

Y eso es todo, me parece muy sencillo si esos ángulos son de 45º, creo que el enunciado debería ser distinto para que fuera un problema más interesante. Ya me dirás si lo interpreté mal.

Hola! muchas gracias solo tengo una duda, 7 ¿porque el lo triangulo derecho no existe?

Yo había supuesto que el ángulo de abajo del primer triángulo era recto, es que en el dibujo es completamente recto. Hagámoslo con las únicas premisas de los ángulos y de la igualdad de los dos lados.

Aprovecharé el mismo dibujo de Lucas al que añadiré un angulo alfa arriba al triángulo izquierdo. Por lo que el arriba a la derecha será (45-alfa), el del triángulo central a la izquierda será (45+alfa) y el del triángulo central a la derecha será (90-alfa)

Aplicando el teorema del seno a todo bicho viviente tendremos:

$$\begin{align}&\frac{a}{sen \alpha}=\frac{m}{sen45º}\\&\\&\frac{b}{sen(45º-\alpha)}=\frac{n}{sen 45º}\\&\\&\frac{x}{sen 45º}=\frac{n}{sen(45º+\alpha)}=\frac{m}{sen(90º-\alpha)}\\&\\&\text{Y ahora a calcular}\\&\\&a^2=\frac{m^2sen^2\alpha}{sen^2 45º}=\frac{\frac{x^2sen^2(90-\alpha)}{sen^245º}·sen^2\alpha}{sen^245º}=\\&\\&\frac{x^2cos^2\alpha·sen^2\alpha}{sen^445º}\\&\\&b^2=\frac{n^2sen^2(45º-\alpha)}{sen^245º}=\frac{\frac{x^2sen^2(45º+\alpha)}{sen^245º}·sen^2(45-\alpha)}{sen^2 45º}=\\&\\&\frac{x^2\left(\frac{\sqrt 2}{2}(\cos\alpha+sen\alpha)  \right)^2 \left(\frac{\sqrt 2}{2}(\cos\alpha-sen\alpha)  \right)^2}{\cos^445º}=\\&\\&\frac{x^2(1+2cos\alpha·sen\alpha)(1-2cos\alpha·sen\alpha)}{4cos^4 45º}=\\&\\&\frac{x^2(1-4cos^2\alpha·sen^2\alpha)}{4sen^445º}\\&\\&\\&a^2+b^2=\frac{x^2cos^2\alpha·sen^2\alpha}{sen^445º}+\frac{x^2(1-4cos^2\alpha·sen^2\alpha)}{4sen^445º}=\\&\\&\frac{4x^2cos^2\alpha·sen^2\alpha+x^2-4x^2cos^2\alpha·sen^2\alpha}{4·\left(\frac{\sqrt 2}{2}\right)^4}=\\&\\&\\&\frac{x^2}{4·\frac{4}{16}}=x^2\\&\\&\end{align}$$

Y eso es todo, espero que te sirva y lo hayas entendido.  Así tienes dos formas de demostrarlo, en esta hya que calcular mucho pero no la veo yo tan rebuscada como la otra.