Calcular el módulo y la dirección

Si son tres vectores dato deberías proceder a sumar las componentes sub x y sub y de cada uno y así obtendrías la resultante...

VactorA = ( 10v2 cos 45 ,   10V2 sen 45) = ( 5  ,   5)

Vector B= ( 10 cos 127 ,   10 sen 127)  = ( -6  ,  7.986 )

Vedtor C = ( 15 cos 270 ,   15 sen 270 ) = ( 0      ,  -15)

Vector resultante = ( -1   ,   -2)

Modulo =V( 1 + 4 ) = V5

Direccion = arc tg (-2) = - 63.43°

Perdón... Replanteo

VactorA = ( 10v2 cos 45 ,   10V2 sen 45) = ( 10  ,   10)

Vector B= ( 10 cos 127 ,   10 sen 127)  = ( -6  ,  7.986 )

Vedtor C = ( 15 cos 270 ,   15 sen 270 ) = ( 0      ,  -15)

Vector resultante = ( 4   ,   2.986)

Modulo = V 16 + 8.916 = 5

dIRECCION = arc. tg. 2.986 / 16 = 10.57°

¡Gracias! Es una excelente respuesta muy clara! Comienzo a entender más el tema

bueno con una duda en direccion deveria ser = tg-1(2.98/4)=36.68

·

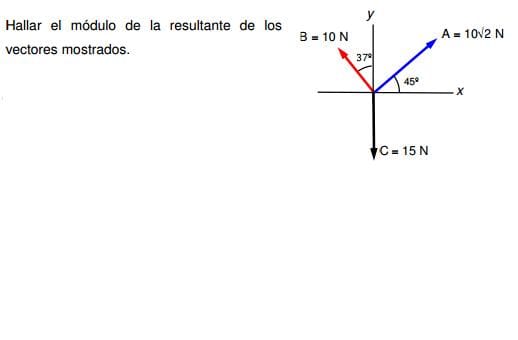
Para sumar vectores descomponemos los vectores en las componentes que tienen en el eje X y el eje Y. Luego se suman entre si las componentes del eje X y las del eje Y con lo cual tienes las componentes del vector resultante. Aquí lo único que puede cambiar entre un matemático y un físico puede ser la notación. Yo me siento mucho más cómodo denotando los vectores como

u=(ux, uy)

que como

u= ux·i + uy·j

Y los vectores serán:

$$\begin{align}&A=(10 \sqrt 2\,\cos 45º,\;10 \sqrt 2\;sen\, 45º)=\\&\\&\left(10 \sqrt 2\,\frac{\sqrt 2}{2},\;10 \sqrt 2\;\frac{\sqrt{2}}2\right)=(10,10)\\&\\&\\&B=(10cos(90º+37º),\;10sen(90º+37º))=\\&\\&(-10 sen\, 37º, 10 \cos 37º)\\&\\&\\&C=(0,\;-15)\\&\\&\\&R=A+B+C=(10-10sen37º,\;10+10 \cos 37º-15)=\\&\\&(10-10\, sen\,37º, \;-5+10 \cos 37º)\approx (3.98185,2.98636)\\&\\&\\&|R|=\sqrt{3.98185^2+2.98636^2}=4.977296\\&\\&\text{Y la dirección es}\\&\\&tg^{-1}\left(\frac{2.98636}{3.98185}  \right)= 36.8696º\end{align}$$

Como coinciden el ángulo que da la calculadora que está en el primer cuadrante y el vector también lo está ya que tiene las dos componentes positivas, ya esta resuelto.  Otras veces no coinciden y al ángulo de la calculadora hay que sumarle 180º para que de el cuadrante donde está el vector.

·

Y eso es todo.

Me queda claro casi todo solo me falto entender la igualdad de B pero la puedo mantener con la suma de los ángulos 90+37