¿Cómo se resuelve este ejercicio por el método de las arandelas?

·

El método de las arandelas o de los discos es el método que yo veo más normal para estos problemas, porque el de los cascarones lo conozco de hace 4 dias. No lo dimos en nuestros estudios. Como su nombre indica se toman objetos circulares casi planos. Mientras que en el método de los cascarones se toman paredes finas de cilindros cuya altura es la función.

Cuando la región gira alrededor del eje x entre los límites x=a, x=b, y las curvas que limitan la región son f(x) y g(x) con f(x)>g(x) la fórmula es.

$$\begin{align}&V=\pi\int_a^b\left([f(x)]^2-[g(x)]^2\right) dx\\&\\&\text{Cuidado con el error frecuente de usar}\\&\left[f(x)-g(x)\right]^2\\&\\&\end{align}$$

Por supuesto que si las funciones f y g se cortan hay que hacer tantas integrales como regiones se forman y sumar las áreas obtenidas.  Si no sabemos cual es la función mayor podemos hacer la integral y si sale negativa tomamos el valor absoluto.

En este ejercio no nos dicen los límites en X asi que se supone que lo que girará es la región definida por las dos curvas.

Además por ser funciones pares sabemos que son simétricas respecto del eje Y y el volumen generado a la derecha ser el mismo que el de la izquierda, multiplicando por 2 el uno se obtiene el total.

Los puntos de corte de las funciones son

x^4=x^2

x^4-x^2 = 0

x^2(x^2-1)

x=0 es una solución

x^2-1=0

x^2=1

x= +-1

Pero por lo que he dicho solo usaremos la del lado derecho y multiplicaremos por 2. Ese 2 lo pongo ya al principio para no olvidarlo.

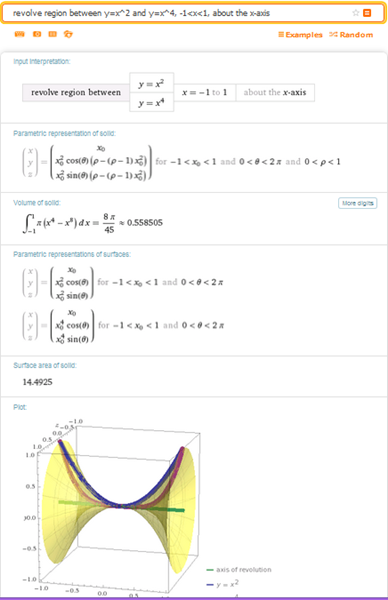
$$\begin{align}&V=2·\pi \int_0^1\left(x^4-x^8  \right)dx=\\&\\&2·\pi\left[\frac{x^5}{5} - \frac{x^9}9  \right]_0^1=\\&\\&2\pi\left(\frac 15 -\frac 19  \right)=2\pi·\frac{9-5}{45}=\\&\\&\frac{8\pi}{45}\approx 0.5585053606\end{align}$$

Y esto es lo que nos da Wolfram Alpha  si ponemos

revolve region between y=x^2 and y=x^4, -1<x<1, about the x-axis

Y eso es todo.