Calcular el volumen del sólido en revolución

Rafa Rojas!

·

Calculemos a mano los puntos de intersección, aunque luego haremos la gráfica y se vean.

x=3-y

3-y=4-(y-1)^2

3-y = 4 -y^2 +2y - 1

y^2 -3y=0

y=0  ==> x=3

y=3  ==> x=0

Luego los puntos de corte son (3,0) y (0,3)

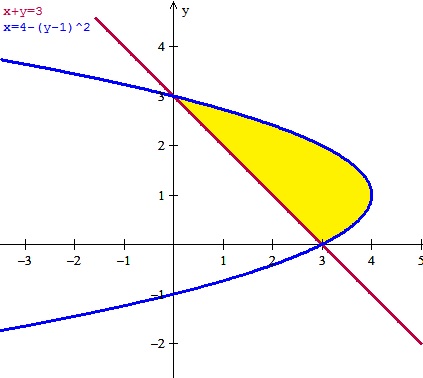
Como girará alrededor del eje X la fórmula es

$$\begin{align}&V=2\pi\int_{y_0}^{y_1}y·f(y)\;dy\end{align}$$

Eso significa que en las funciones debe estar despejada x

x=f(y)

Luego las funciones serán

x = f(y) = 3 - y

x = g(y) = 4-(y-1)^2

g(y)= 4 -(y-1)^2 es la que crea el volumen exterior

f(y) = 3-y es la que crea el volumen interior que debe ser restado.

Y los límites son los de la proyección de la figura en el eje Y que son 0 y 3

Con todo esto el volumen sería

$$\begin{align}&V=2\pi\int_0^3y[g(y)-f(y)]dy=\\&\\&2\pi\int_0^3y[4-(y-1)^2-3+y]dy =\\&\\&2\pi \int_0^3y(4-y^2+2y-1-3+y)dy=\\&\\&2\pi\int_0^3y(-y^2+3y) dy=\\&\\&2\pi\int_0^3(-y^3+3y^2)dy=\\&\\&2\pi\left[ -\frac{y^4}{4}+y^3 \right]_0^3=\\&\\&2\pi\left(-\frac{81}{4}+27  \right)=\\&\\&2\pi·\frac{27}{4}=\frac{27\pi}{2}\approx42.41150082\end{align}$$

·

Y eso es todo.