Como resolver problema Matematica Discreta
El problema dice asi :
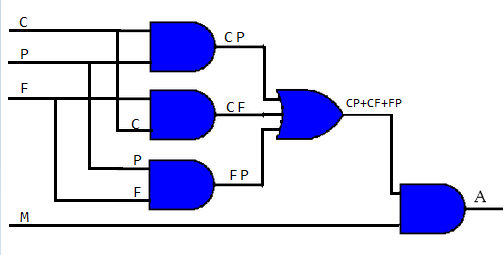
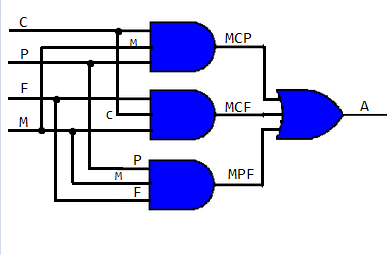
Un tribunal de seleccion para el ingreso en una empresa de procesos informaticos debe examinar los expedientes de un gran numero de candidatos. El criterio de admision es el siguiente :un alumno es admitido si y solamente si el candidato alcanza la nota minima en matematicas discreta y en un minimo de dos de las siguientes disciplinas :Calculo I, Programacion y Fisica I .Escribe una expresion Booleana que efectue la seleccion, simplificacion y construye un circuito que efectue automaticamente dicha seleccion .
Nota : Asumir el valor de "0" si desaprueba y "1" si aprueba el curso
1 respuesta
Llamaremos
M = alcanzar nota mínima en matemática discreta
C = alcanzar nota mínima en Calculo I
P = alcanzar nota mínima en Programación
F = alcanzar nota mínima en Fisica I
Para ser admitido se necesita que sea verdadera esta expresión, donde la operación + es la operación lógica "O" y la operación · (que no se escribe) es la operación lógica "Y"
LLamemos A = ser admitido
A = M(CP+CF+PF)
A lo que voy a hacer yo no lo llamaría simplificación, pero...
A = MCP + MCF + MPF
Este es el circuito
Y eso es todo.
Hola vale, gracias por la respuesta si lo llegue a entender, pero me gustaría saber si el problema lo podemos resolver por el mapa de karnaugh
Si, puede resolverse por el mapa de Karnaugh, aunque eso es para operaciones al azar o de condiciones muy complicadas, aqui de las condiciones que nos piden para ser aceptado se deduce enseguida la expresión Booleana
M C P F | A 0 0 0 0 | 0 0 0 0 1 | 0 0 0 1 0 | 0 0 0 1 1 | 0 0 1 0 0 | 0 0 1 0 1 | 0 0 1 1 0 | 0 0 1 1 1 | 0 1 0 0 0 | 0 1 0 0 1 | 0 1 0 1 0 | 0 1 0 1 1 | 1 1 1 0 0 | 0 1 1 0 1 | 1 1 1 1 0 | 1 1 1 1 1 | 1
Y tenemos
A = MC'PF + MCP'F + MCPF' + MCPF
Y si dibujas el diagrama de Karnaugh verás que MCPF hace pareja con cualquiera de los tres primeros dando estos
A = MPF + MCF + MCP
MC 00 01 11 10 PF 00 01 1 11 1 1 10 1
MCPF es el que está rodeado por los otros tres.
Yo hice el circuito como mejor me parecía. Si tienes que hacerlo adaptado a
A = MPF + MCF + MCP
Tendrás que meter el M en las tres puertas primeras y no meterlo en la última.
