Como resolver Inecuaciones con valor absoluto y quebrados

Al sacar las barras de valor absoluto da lugar a dos inecuaciones diferentes:

$$\begin{align}&\frac{3+|2x+7|+x}{x} \geq3\\&\\&A)Si \ 2x+7>0 \Rightarrow x>\frac{-7}{2} \ la \ inecuacion \ queda\\&\frac{3+2x+7+x}{x} \geq 3\\&\\&\frac{3x+10}{x} \geq3\\&\\&\frac{3x+10}{x}-3 \geq0\\&\\&\frac{3x+10-3x}{x} \geq0\\&\\&\frac{10}{x} \geq0 \Rightarrow x>0\\&ya \ que \frac{+}{+}>0\\&Solucion=(0,+\infty)\\&\\&B)\\&Si\ 2x+7<0 \Rightarrow x<\frac{-7}{2}=-3.5\\&La \ inecuación \ queda:\\&\frac{3-2x-7+x}{x} \geq3\\&\frac{-4-x}{x} \geq3\\&\\&\frac{-4-x}{x} -3 \geq 0\\&\\&\frac{-4-x-3x}{x} \geq 0\\&\\&\frac{-4-4x}{x} \geq 0\\&\\&Un \ cociente \ es \ positivo \ si \ el \ numerador \ y \ denominador\\&tienen \ el \ mismo \ signo:\\&cas1) \\&ha \ de \ verificar \ el \ sistema:\\&-4-4x>0\\&x>0  \\&Imposible , \ ya \ que  \ x<-3.5\\&caso2)\\&ha \ de \ verificar \ el \ sistema:\\&-4-4x<0\\&x<0\\&\\&-4-4x<0 \Rightarrow  -4x<4 \Rightarrow x>-1\\&Imposible , \ ya \ que  \ x<-3.5\\&\\&\end{align}$$

Luego la solución són todos los positivos (0,infinito)

·

Se deben examinar varios casos particulares y luego la respuesta es la unión de las respuestas.

Para empezar separaremos los casos x>0 y x<0. El caso x=0 no existe ya que habría una división por 0.

1)

Si x>0

Entonces se puede pasar la x a la derecha respetando el signo de la desigualdad

$$\begin{align}&3+|2x+7|+x\ge3x\\&|2x+7|\ge2x-3\\&\\&como \;x\gt 0 \implies2x+7\gt0\\&\text {y podemos quitar el valor absoluto} \\&\\&2x+7\ge2x-3\\&7\ge -3\\&\\&\text{que es verdad siempre, luego}\\&\text{todo x}\gt0 \text{ es solución}\\&x \in(0,\infty)\end{align}$$

2)

Si x<0

Entonces al pasar la x a la derecha se invierte el signo de la desigualdad.

$$\begin{align}&3+|2x+7|+x\le3x\\&|2x+7|\le2x-3\\&\\&\text{Ahora hay que separar dos casos:}\\&2a)\quad Si\; x\in\left[-\frac 72 ,0 \right)\\&x\ge - \frac 72\implies2x\ge-7\implies2x+7\ge0\\&\text{y podemos quitar el valor absoluto}\\&2x+7\le 2x-3\\&7\le -3\\&\text{eso es falso, luego no hay solución en [-7/2,0)}\\&\\&\\&2b)\quad Si\; x\lt-\frac 72\\&2x\lt-7\implies2x+7\lt0\\&\text{para quitar el valor absoluto hay que}\\&\text{cambiar de signo lo de dentro}\\&-(2x+7)\le2x-3\\&-2x-14\le2x-3\\&-4x\le11\\&x\ge \frac {11}4\\&\text{pero no sirve porque debía ser }x\lt-\frac 72\\&\text{luego no hay soluciones para }x\lt -\frac 72\end{align}$$

Resumiendo, para x<0 no hay salución.

·

Luego la solución es

$$\begin{align}&S=(0,\infty)  \quad \quad \\&\text{o dicho de otro modo} \\&S=\mathbb R^+\end{align}$$

Y siempre está bien tener una prueba de que se ha hecho bien porque en estos ejercicios te puedes líar.  Graficaré la función

y=(3+|2x+7|+x)/x - 3

La cual será positiva cuando se cumpla la inecuación inicial.

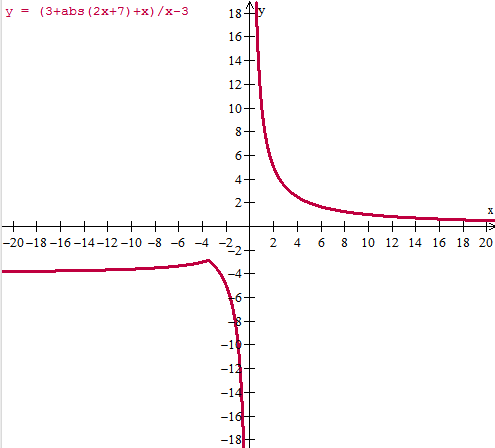
Y efectivamente, confirma que la solución que he dado es la buena.