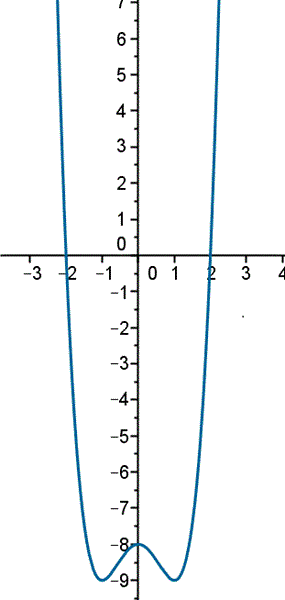Resolver desigualdad y escribir Intervalos con Grafica
HolaValeroasm
Quisiera que me puedas ayudar con este problema.
- Resolviendo
- Intervalos
- Gráfica
La gráfica si me será muy necesaria para poder entender un poco más.
$$x^4-8=2x^2$$
1 respuesta
No entiendo el problema. Pides resolver una desigualdad pero lo que me escribes es una ecuación, es necesario que haya una desigualdad. Te digo como se escriben los signos de desigualdad el Látex por si los necesitas.
\lt menor
\le menor o igual
\gt mayor
\ge mayor o igual
\ne distinto
Por ejemplo:
x^4-8 \le = 8x^2
$$x^4-8\ge 2x^2$$
´Perdon, je je esta es el verdadero :)
Ahora si.
Pasamos todo a un lado
x^4 - 2x^2 - 8 >= 0
Es una ecuación bicuadrada, para hallar las raíces hacemos
y=x^2
y^2 - 2y - 8 >=0
y = [2 +- sqrt(4+32)] / 2 = (2 +- 6) / 2 = 4 y -2
x = +- sqrt(y)
x = +- 2
La raíz de -2 es compleja no nos sirve, la curva solo corta el eje X en los puntos 2 y -2.
Como es una función continua el signo entre los cortes será constante, para averiguarlo basta
Calcular en un punto intermedio.
x^4 - 2x^2 - 8 >= 0
Entre -infinito y -2 el signo es positivo porque el límite en menos infinito es más infinito. Luego ese tramo cumple la desigualdad.
Entre -2 y 2, probemos con el cero, el resultado es -8 que no cumple la desigualdad
Entre 2 y +infinito el signo es positivo porque el limite en +infinito es +infinito, luego se cumple.
Como la desigualdad incluye la igualdad entraran las raíces donde la función vale cero.
La solución es:
(-infinito, -2] U [2, +infinito)
La gráfica es la de la función
y = x^4 - 2x^2 -8
Se hace dando unos cuantos puntos o mucho mejor con un programa de ordenador. Es fea para la web porque es muy empinada y solo veremos un franja vertical estrecha.
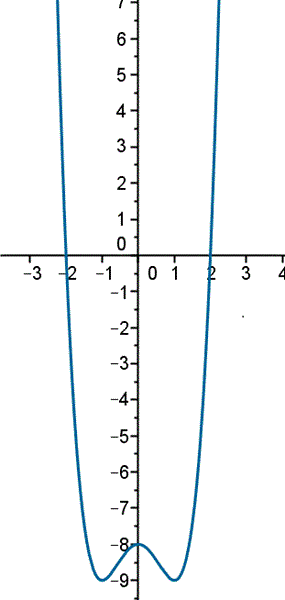
Se ve perfectamente donde es positiva la función que es donde se cumple la desigualdad y donde es negativa y no se cumple.
Y eso es todo.
