Hallar el centroide de la región que tiene como fronteras las rectas y=2x+1, x+y=7, x=8

·

¿De qué forma se supone que hay que hacerlo? Con integrales de la masa por la distancias en X y Y divididas entre la integral de la masa, o como la intersección de las medianas del tríangulo que se forma.

Con integrales de la masa por las distancias en X y Y 

Vamoa a hacer la gráfica:

Calculamos las coordenadas de los puntos:

A = intersección b, c

x=8

y=7-8 = -1

A(8, -1)

·

B=intersección a, b

x=8

y=2·8+1=17

B(8,17)

·

C=intersección a, b

y=2x+1

x+y=7

restando primera a segunda

x = 7-2x-1

3x=6

x=2

y=7-2=5

·

Las fórmulas del centro de masas son

$$\begin{align}&x_c=\frac{\iint_R x\,\gamma(x,y,z)dydx}{\iint_R\gamma(x,y,z)dydx}\\&\\&y_c=\frac{\iint_R y\,\gamma(x,y,z)dydx}{\iint_R\gamma(x,y,z)dydx}\\&\\&\text{donde }\gamma(x,y,z) \text{es la función de densidad}\\&\text{En este es constante y la suponemos 1}\\&\\&x_c=\frac{\iint_R x\;dy\,dx}{\iint_Rdy\,dx}\\&\\&y_c=\frac{\iint_R y\;dy\,dx}{\iint_R dy\,dx}\\&\\&\\&\iint _Rx\;dy\;dx=\int_2^8\int_{7-x}^{2x+1}x\;dy\,dx=\\&\\&\int_2^8 x·y\bigg|_{7-x}^{2x+1}\,dx=\int_2^8x(2x+1-7+x)dx=\\&\\&\int_2^8(3x^2-6x)dx=\left[x^3-3x^2  \right]_2^8=\\&\\&512-192-8+12=324\\&\\&\\&\\&\iint _Ry\;dy\;dx=\int_2^8\int_{7-x}^{2x+1}y\;dy\,dx=\\&\\&\int_2^8 \frac{y^2}2\bigg|_{7-x}^{2x+1}\,dx=\\&\\&\frac 12\int_2^8(4x^2+4x+1-49+14x-x^2)dx=\\&\\&\frac 12\int_2^8(3x^2+18x-48)dx=\\&\\&\frac 12\left[x^3+9x^2-48x  \right]_2^8\\&\\&\frac 12\left(512+576-384-8-36+96\right)=\\&\\&\frac 12·756=378\\&\\&\\&\\&\iint _Rdy\;dx=\int_2^8\int_{7-x}^{2x+1}dy\,dx=\\&\\&\int_2^8y\bigg|_{7-x}^{2x+1}dx=\int_2^8(2x+1-7+x)dx=\\&\\&\int_2^8(3x-6)dx=\left[ \frac{3x^2}{2}-6x \right]_2^8=\\&\\&96-48-6+12=54\\&\\&\\&x_c=\frac{324}{54}=6\\&\\&y_c=\frac{378}{54}=7\\&\\&\text{centroide=}(6,7)\end{align}$$

Y eso es todo, no sé si por intesección de medianas cuesta máas o menos.  Pero si estás en el tema de aplicaciones de las integrales múltiples es lógico que se tenga que resolver así.

Veamos primero con una imagen las rectas que te piden y el área que delimitan, para entender que te están pidiendo

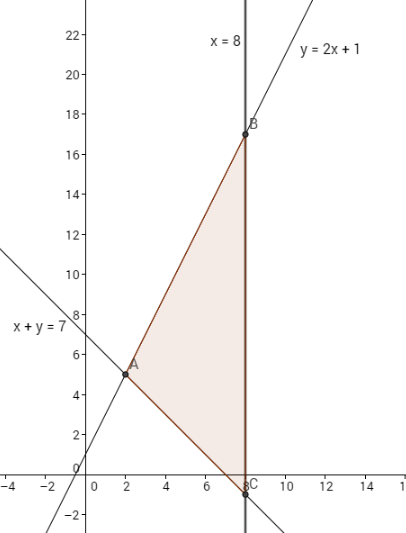
Como se forma un triángulo, lo que vamos a hallar es el baricentro (punto donde se cruzan las 3 medianas del triángulo)

Empecemos por hallar los vértices del mismo (puntos A, B, C) que son las intersecciones de las rectas que nos dan

Punto A
x+y=7---> y = 7-x

y=2x+1

2x+1 = 7-x

3x = 6 ---> x = 2

y = 5

A = (2, 5)

Punto B

y = 2x+1

x = 8

y = 2*8+1 = 17

B = (8, 17)

Punto C

x+y = 7

x = 8

y = -1

C = (8, -1)

La mediatriz del segmento BC es fácil de hallar, ya que se encuentran sobre una recta horizontal

en x, obviamente va a ser 8; y en y va a ser (17 + -1) / 2 = 8

Así que el baricentro va a estar sobre los puntos del segmento que va del punto A, a este punto recien hallado (8,8).

Veamos la forma que tiene recta directriz de ese segmento.

Los puntos conocidos son (2, 5), (8, 8)

La expresión de la recta

(y-y0) / (y1-y0) = (x-x0) / (x1-x0)

(y-5)/(8-5) = (x-2) / (8-2)

y = x/2 + 4

Hay que hacer lo mismo con los otros dos segmentos (en realidad alcanzaría solo con uno) para hallar la recta directriz de otro mediana y cuando tengas las 2 rectas, las igualas para hallar los puntos.

Intenta resolver esto último y cualquier duda comenta.

Te dejo un poco más de detalle. El punto sobre el segmento AC es el punto medio de los valores (2, 5) y (8, -1), si calculas la media para cada valor obtenés el punto (5, 2) que es el que tenés que unir con el punto B para ver la expresión de esa recta. Haciendo lo mismo que antes obtenemos

(y-2) / (17-2) = (x-5) / (8-5)

que llegás a la expresión y = 5x-23

igualando esa recta con la recta y = x/2 + 4

Obtenemos

5x-23 = x/2 + 4

(9/2) x = 27

x = 6

y reemplazando y = 7

Por lo tanto el baricentro es (6, 7)

En mi ejercicio me pide calcular el área y realizar su integra, además me pide calcular My, Mx.  Y que se obtenga el resultado de estas. Me podría apoyar por favor.