¿Como se hace esta integral? :)
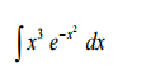
Muchas gracias por vuestro tiempo :)
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
2 Respuestas
Respuesta de Lucas m
1
Respuesta de Valero Angel Serrano Mercadal
1
