Calcular la integral triple sobre una región R
¿Quisiera saber el procedimiento paso a paso para resolver esto creo falta algún dato para acotar el volumen? ¿Cuál es el resultado?
Calcular la integral triple de F(x,y,z)=z sobre la region R en el primer octante acotado por los planos y=0, z=0 , x+y=2, 2y+x=6 , y el cilindro y^2 +z^2=4
1 respuesta
·
Hay que echarle un poco de imaginación ya que las gráficas tridimensionales no están muy al alcance, yo no he conseguido un programa bueno para ellas.
El cilindro y^2+z^2=4 está tumbado y centrado en el eje X y su radio es 2.
Si nos dicen primer octante ya no es necesario que nos digan acotado por y=0, z=0 ya que primer octante incluye las condiciones x>=0, y>=0, z>=0
Y los planos
x+y=2
2y+x=6
son verticales al carecer de z.
Vamos a dibujar el dominio de integración que eso si es fácil, es la proyección sobre el plano z=0 de todo lo que tenemos.
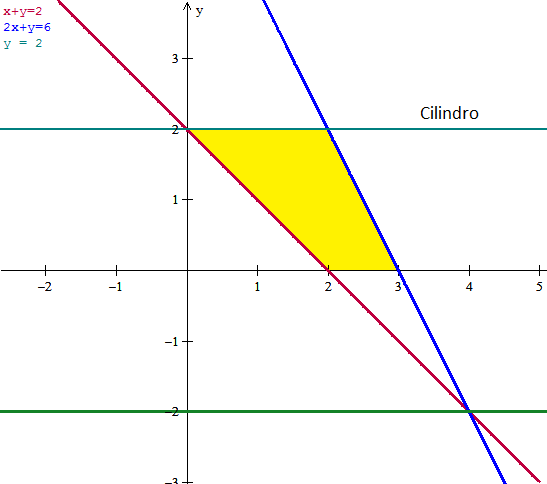
Lo marcado en amarillo es el dominio. Para hacerlo con una sola integral tomaremos como límites fijos los de y, entre 0<=y<=2
Y como límites variables en x los de las dos rectas dadas como función x=f(y)
x=2-y
x=(6-y)/2
2-y <= x <= (6-y)/2
Y los límites en z son los de suelo y la pared del cilindro expresada como función z = f(x, y). Serán
0 <= z <= sqrt(4-y^2)
Luego el volumen expresado como integral triple es
$$\begin{align}&V=\int_0^2\int_{2-y}^{\frac{6-y}2}\int_0^{\sqrt{4-y^2}}dz\,dx\,dy\end{align}$$Y esto convendría que lo integrases tú.
Veo que hiciste la integral, por si acaso te digo cual es la respuesta
$$\begin{align}&V=\pi+\frac 43\end{align}$$
