Como se utilizan las particiones en las sumas de Riemann
No entiendo por que se asignan los valores en x0, x1, x2... Además de no saber como se utilizan los valores de w1, w2... La evaluación seria en un rango de 0, 3 donde a seria 0 y b=3 eso creo, me podrían ayudar

1 Respuesta
Respuesta de Valero Angel Serrano Mercadal
1
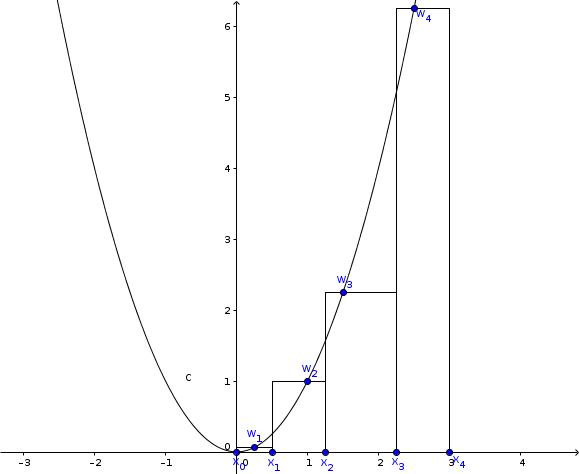


Que pasa con x0=0 sera posible Sr. Valero que explique paso a paso como acomoda la operación! - Marco Rodriguez