Se tiene la siguiente función, variables aleatorias, discretas y continuas
Se tiene la siguiente función
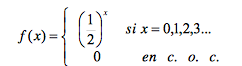
a) Verifique si la función es una función de masa de probabilidad. En caso afirmativo:
b) Determine las siguientes probabilidades: P(X=3); P(X>2); P(X < 2)
c) ObtengalafunciónacumuladadeprobabilidadF(x)
1 Respuesta
Respuesta de Valero Angel Serrano Mercadal
2
