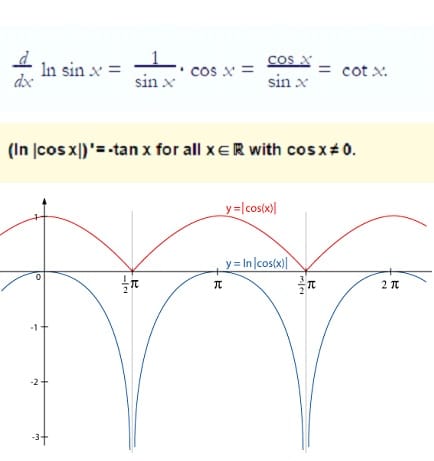
Gráficas calculo integral curvan intervalo
Buenas noches amigos de todo expertos sigo con mi taller de calculo espero me ayuden con la gráfica
2 respuestas
Respuesta de Wilmer Encarnacion
2
- http://www.themathpage.com/aCalc/exponential.htm
- http://www.tomsmath.com/step-by-step-directions-for-finding-the-derivative-of-lncosx.html
Siempre es bueno que investigues, análisis y saques tus conclusiones.
Respuesta de Lucas m
2
La longitud de una curva se calcula con la integral:
$$\begin{align}&L=\int_a^b \sqrt{1+[f(x)']^2 }dx\\&\\&D(lncosx)=\frac{1}{cosx}(-senx)=-tanx\\&\\&=\int_0^{\frac{\pi}{3}} \sqrt{1+tan^2x}\ \ dx=\int_0^{\frac{\pi}{3}}\sqrt{ sec^2(x)} \ \ dx=\int_0^{\frac{\pi}{3}}secx ·dx=\\&\\&\\&=\Bigg[ln \Big|secx+tanx \Big| \Bigg]_0^{\frac{\pi}{3}}=ln \Big|2+ \sqrt 3 \Big|-ln \Big|1+0 \Big|=\\&\\&=ln \Big|2+ \sqrt 3 \Big| \simeq1.316957897....\end{align}$$Saludos
;
;