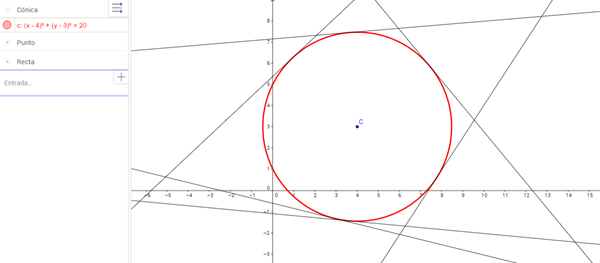
Problema de geometria analitica ecuacion

Falta algún dato más ya que la circunferencia tiene infinitas tangentes (si no ponés otra condición). Dibujá una circunferencia en cualquier lado y empezá a "tirar rectas tangentes", verás que si no ponés otra condición, podés encontrar muchas rectas que sean tangentes...

Salvo que te pregunten la ecuación general de todas las rectas que sean tangentes a esa circunferencia.

solo eso me indicaron, pero una duda. no se puede lograr obtener por medio de los ejes, solo me piden hallar la ec de la tangente a la circunferencia dada

Te falta indicar el punto de tangencia.

La pendiente de la tangente se calcula con la derivada.

Se tendría que derivar implícitamente:

$$\begin{align}&x^2-8x+y^2-6y+5=0\\&\\&2x-8+2yy'-6y'+0=0\\&\\&Factor \ común \ a \ y':\\&y'(2y-6)=8-2x\\&\\&y'=\frac{8-2x}{2y-6}\end{align}$$

El punto lo sustituyes en la derivada y tendrás la pendiente.

Con el punto y la pendiente escribes la ecuación de la recta tangente:

$$\begin{align}&punto \ de \ tangencia: T=(x_0,y_0)\\&\\&y-y_0=m(x-x_0)\\&\\&m_t=y'(x_0)\end{align}$$

Indícame el punto de tangencia y lo acabamos

Saludos

;

;

Recuerda: las derivadas de las funciones sirven para calcular pendientes de las rectas tangentes a esas funciones