Tengo una duda sobre estos problemas de doble integración

5.-c)

Observa que la integral interior

$$\begin{align}&\int e^{x^2}dx \ \ NO \ TIENE \ ANTIDERIVADA\end{align}$$

Tendremos que cambiar el orden de integración:

$$\begin{align}&\int_{y=0}^{y=4}  \Bigg\{ \int_{x=y/2}^{x=2} e^{x^2}dx \Bigg \}dy\end{align}$$

Es un Recinto Tipo II: y entre números,x entre curvas.

Si queremos cambiar el orden de integración también tendremos que cambiar la partición del recinto a uno Tipo I (x entre números y entre curvas)

Dibujo el recinto:

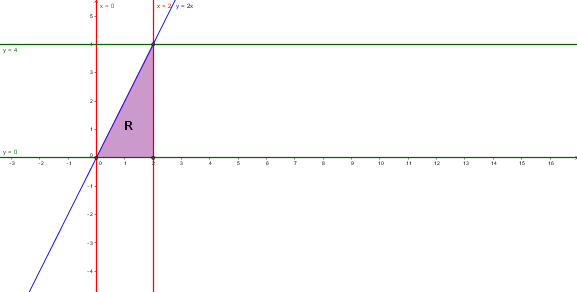
Al cambiar a un Recinto Tipo I (x entre números):

0<=x<=2

Las y variaran (observa el Recinto morado) entrando de abajo arriba

desde  y=0 (eje X) a la recta y=2x ( se obtiene del límite de integración x=y/2 , despejando la y)

Entonces al cambiar el orden de integración la integral quedará:

$$\begin{align}&\int_{x=0}^{x=2} \Bigg \{ \int_{y=0}^{y=2x} e^{x^2}dy \Bigg \}dx=\\&\\&= \int_{x=0}^{x=2} \Bigg  [ e^{x^2}y \Bigg ]_{y=0}^{y=2x} dx=\\&\\&= \int_{x=0}^{x=2} e^{x^2} \Big(2x-0 \Big)dx=\\&\\&= \int_{x=0}^{x=2} 2x e^{x^2}dx=\\&\\&= \Bigg[e^{x^2} \Bigg ]_0^2=e^4-e^0=e^4-1=53.5982..\end{align}$$

Saludos

;

;