·
·
¡Hola Julio!
Haré el primero de los ejercicios, los otros deberás mandarlos en otras preguntas distintas si no te los quiere hacer otra persona.
a)
Se trate de un polinomio, es una función que apenas tiene problemas porque esta definada en todo R, es continua en todo R, no tiene periodicidad y no tiene asíntotas de ningun tipo.
Lo que tienen algunas veces es simetria respecto del eje Y o simetría central.
Esta vez tiene simetría respecto al eje Y ya que
f(x)=f(-x)
Eso se debe a que solo tiene términos de grado par que dan el mismo valor en x y en -x.
Otra cosa que se busca son los cortes con los ejes.
Inmediatamente se ve que con el eje Y se corta en (0,0) el cual a la vez también es un corte para el eje X.
Y los otros cortes con el eje X los calculamos resolviendo la ecuación
x^4 - 4x^2 = 0
x^2·(x^2-4) = 0
De x^2=0 sale x=0 que ya lo habíamos contemplado antes
De (x^2 - 4) = 0 sale
x^2 = 4
x = -2 y 2
Luego los cortes con el eje X son:
{(-2,0), (0,0), (2,0)}
·
Y vamos ya con las derivadas para calcular máximos, mínimos y crecimiento o decrecimiento
f(x) = x^4 - 4x^2
derivamos e igualamos a 0
f '(x) = 4x^3 -8x =0
x(4x^2 - 8)=0
x=0
4x^2=8
x^2=2
x = - sqrt(2) y sqrt(2)
luego los puntos críticos son tres, {-sqrt(2), 0, sqrt(2)}
Por simetria sabemos que en -sqrt(2) y sqrt(29 será lo mismo
Calculamos la derivada segunda
f ''(x) = 12x^2 - 8
f''(sqrt(2)) = 12·2 - 8 = 24 - 8 = 16 es mínimo, lo mismo que en -sqrt(2)
el máximo es
f(sqrt(2)) = 4 - 8 = -4
luego tenemos estos mínimos (-sqrt(2), -4), (sqrt(2), -4)
f''(0) = -8 es máximo
Y el máximo (relativo) es el punto (0,0)
·
Entonces de acuerdo a esta configuración de máximos y minímos tenemos.
(-Infinito, -sqrt(2)) la función decrece
(-Sqrt(2), 0) creciente
(0, sqrt(2)) decreciente
(Sqrt(2), infinito) crece
·
Y ahora veamos si hay puntos de inflexión, son los que anulan la derivada segunda.
f ''(x) = 12x^2 - 8=0
12x^2 = 8
x^2 = 2/3
x=-sqrt(2/3) y sqrt(2/3)
El valor de la función en ellos es
f(sqrt(2/3)= 4/9 - 8/3 = -20/9
luego son los puntos
(-sqrt(3/2), -20/9) y (sqrt(2/3), -20/9)
Veamos la concavidad
(-infinito, -sqrt(2/3)) tomamos x=-1 entonces f''(-1) =12-8=4 la función es cóncava hacia arriba
(-sqrt(2/3), sqrt(2/3)) tomamos x=0 entonces f''(0) = -8 la función es cóncava hacia abajo
(sqrt(2/3), infinito) tomamos 1 entonces f''(1)=4 la función es cóncava hacia arriba.
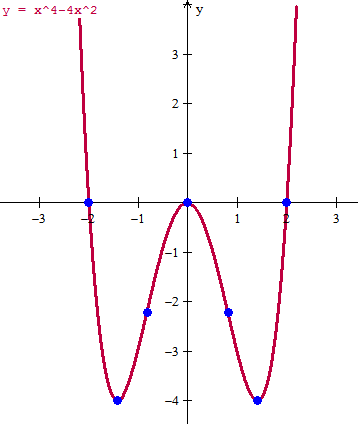
Y con todos estos datos se debería ser capaz de bosquejar la función, yo voy a hacerla con un programa y así puedes comparar lo que te saldría sin usarlo.
Todos los puntos marcados en azul se han calculado en lo que he hecho.
:
:



