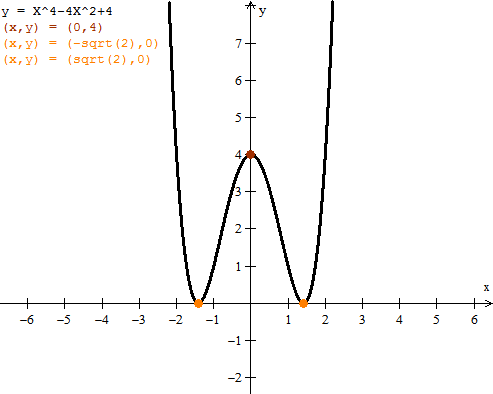Como resolver: Máximos, mínimos y gráfica de una función

·

·

¡Hola Julio!

Ahora no podré hacer la gráfica, más tarde.

$$\begin{align}&f(x)=x^4-4x^2+4\\&\\&f'(x)=4x^3-8x=0\\&\\&x(4x^2-8)=0\\&x_1=0\\&\\&4x^2-8=0\\&4x^2=8\\&x^2=2\\&\\&x_2= \sqrt 2\\&x_3=-\sqrt 2\\&\\&\text{Calculamos la derivada segunda}\\&f''(x)=12x^2-8\\&\\&\text{Y evaluamos los puntos críticos}\\&\\&f''(0) = -8 \implies máximo\\&\\&f''(\sqrt 2)=24-8=16\implies mínimo\\&f''(-\sqrt 2)=24-8=16\implies mínimo\\&\\&\text{Luego el máximo relativo es}\\&\\&(0,f(0)) = (0,4)\\&\\&\text{Y los mínimos relativos son}\\&\\&(\sqrt 2,f(\sqrt 2))=(\sqrt 2, 4-8+4)=(\sqrt 2,0)\\&(-\sqrt 2,f(-\sqrt 2))=(-\sqrt 2, 4-8+4)=(-\sqrt 2,0)\end{align}$$

Y eso es todo de momento.

Saludos.

:

: