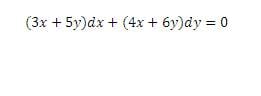Ecuaciones homogéneas con variables separables

·

·

¡Hola Brenda!

Primero la ponemos en la forma

dy/dx = f(x,y)

$$\begin{align}&(3x+5y)dx +(4x+6y)dy=0\\&\\&(4x+6y)dy=-(3x+5y)dx\\&\\&\frac {dy}{dx}=-\frac{3x+5y}{4x+6y}\\&\\&\text{Puedes comprobar fácilmente que es homogénea}\\&\\&f(\lambda x,\lambda y)=-\frac{3\lambda x+5\lambda y}{4\lambda x+6\lambda y}=-\frac{3x+5y}{4x+6y}=f(x,y)\\&\\&\text{Hacemos el cambio }y=ux\\&\\&\frac{dy}{dx}=\frac{du}{dx}·x+u=-\frac{3x+5ux}{4x+6ux}=-\frac{3+5u}{4+6u}\\&\\&\text{nos quedamos con esto}\\&\\&\frac{du}{dx}·x+u=-\frac{3+5u}{4+6u}\\&\\&\frac{du}{dx}·x=-\frac{3+5u}{4+6u}-u=\frac{-3-5u-4u-6u^2}{4+6u}\\&\\&\frac{6u+4}{6u^2+9u+3}du=-\frac{dx}{x}\\&\\&\text{La integral izquierda llevará algo de trabajo}\\&\\&\int \frac{6u+4}{6u^2+9u+3}du=\\&\\&u=\frac{-9\pm \sqrt{81-72}}{12}= -1 \quad y - \frac 12\\&\\&\text {el factor } \frac 16 \text{ lo meteré en la segunda}\\&\text{de las fracciones simples}\\&\\&\frac a{u+1}+\frac b{6u+3}=\frac{(6a+b)u+3a+b}{6u^2+9u+3}\\&\\&6a+b=6\\&3a+b=4\\&\\&\text{restando}\\&\\&3a=2\implies a=\frac 23\implies b=4-2=2\\&\\&=\frac 23\int \frac{du}{u+1}+2\int \frac{du}{6u+3}=\\&\\&\frac 23 ln(u+1)+\frac 23\int \frac {du}{2u+1}=\\&\\&\frac 23 ln(u+1)+\frac 13 ln (2u+1)\\&\\&\text{Luego la solución es}\\&\\&\frac 23 ln(u+1)+\frac 13 ln (2u+1)=-ln\,x+ln\,C\\&\\&ln\left((u+1)^{\frac 23}·(2u+1)^\frac 13  \right)=ln \frac Cx\\&\\&(u+1)^{\frac 23}·(2u+1)^\frac 13 =\frac Cx\\&\\&\left(\frac yx+1\right)^{\frac 23}·\left( \frac {2y}x+1\right)^\frac 13 =\frac Cx\\&\\&\sqrt[3]{\frac{(y+x)^2}{x^2}·\frac{2y+x}{x}}=\frac Cx\\&\\&\sqrt[3]{(y+x)^2(2y+x)}= C\\&\\&(y+x)^2(2y+x)= C\\&\end{align}$$

Y eso es todo, repásalo porque es fácil haberse equivocado.

Saludos.

:

: