Solenoide dentro de un campo magnético
Me podrían explicar el procedimiento a seguir detalladamente por favor: Les agradezco su tiempo y de nuevo muchas gracia por contestar.
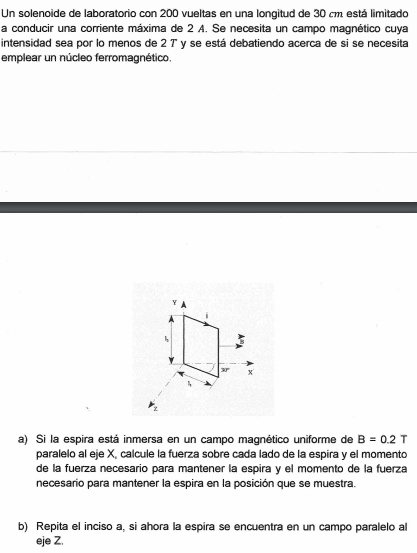
El angulo es de 30° por si no se alcanza a ver, I1 es la flecha de abajo e I2 es la flecha de la izquierda del rectángulo paralela al eje Y.
2 respuestas
Respuesta al primer problema.
La induccción magnética creada por un solenoide es:
https://es.wikipedia.org/wiki/Solenoide
En el caso concreto B = 4 pi 10^-7 x 200 x 2 / 2 x 0,03 = 8,377 mT (4 pi 10^-7 es la permeabilidad magnética del aire).
Valor muy alejado del deseado de 2 T, por lo cual se impone la necesidad de un núcleo magnético, que tendrá una permeabilidad mucho más alta que la del aire.
Erika... No se entiende bien... Primero hablas de una inducción de 2 Tesla dentro de una bobina tipo solenoide ( como un resorte) de 30 cm. De largo y 200 espiras.
Pero más abajo el tema es totalmente distinto... única espira cuadrada sumergida en una inducción fija de 0.20 T. en el aire... pero no das dimensiones físicas por lo que la solución seria como función de los lados y del angulo de inclinación.
¿Son dos preguntas distintas?
Aclara estos puntos para poder proceder más adecuadamente.
Según me parecería es el segundo enunciado... te adelanto planteo .
Es una espira única. Supone que circula una corriente I ( A) ... Tienes que analizar las fuerzas sobre cada lado de la espira.
Para los lados l1 ( horizontales) las fuerzas te saldrán del producto vectorial :
F = I l1 x B... como es producto vectorial las fuerzas sobre cada lado serán iguales en modulo a... I l1 B sen ( angulo entre l1 y B) = I l1 B sen 30° = 0.50 x 0.20 x I l1 = 0.10 Newton... serán iguales pero opuestas ( porque la corriente se invierte ) o sea se cancelarian mutuamente.
Para los lados l2 ( verticales) las fuerzas también serán iguales y opuestas con valor :
F ( l2) = I l2 B sen 90° = I l2 x 0.20 = 0.20 I l2 Newton. Pero ahora estas fuerzas opuestas forman un par o momento que tiende a girar a la espira hasta ponerla perpendicular al vector B.
El momento sobre la espira lo hallarías planteando .
Momento ( respecto eje z) = 0.20 I l2 x l1 x cos 30° = 0.20 x 0.866 x I x l1 x l2 Nm.
Para un campo B paralelo al eje z... replanteas todo como antes con alfa = 60° y sin mover la espira.