Un ejercicio con la Transformada de Laplace
Realmente no entiendo bien este tema espero y puedan ayudarme con este ejercicio
El ejercicio me piden calcular la siguiente transformada de Laplace y comprobar que se cumplen las dos condiciones para la existencia de la transformada de Laplace de la función f(x).
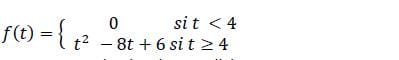
2 Respuestas
Respuesta de Valero Angel Serrano Mercadal
1
Respuesta de Jorge Herrera

