Determinar los extremos relativos, puntos de inflexión y graficar de la siguiente función.

·

·

¡Hola Ana Belén!

Si puntuas normal respuestas como estas:

Desarrolla las siguientes derivadas utilizando las fórmulas y reglas de derivación

Pensamos que es imposible conseguir la nota de Excelente y que quizá esperes una respuesta mejor, por lo cual no contestaríamos.

Ahora bie, si subes esa nota a Excelente es cuando pensamos que merece la pena responderte y lo haremos.

Saludos.

:

:

Una disculpa, no sabia que eso afectaba. Ya cambie la puntuación. Muchas gracias.

Disculpada. Lo que te pediría es que no puntúes a Jorge Herrera que no le he visto resolver en mi vida un solo ejercicio de matemáticas y lo único que hace es mandar siempre la misma retahíla de videos, yo pienso que no se merece nada.

Los extremos relativos son los puntos donde en un entorno de ese punto todos los valores de la función son o bien todos mayores o bien todos menores que el valor de la función en ese punto. Si se da lo primero es un máximo relativo y si se da lo segundo es un mínimo relativo.

En funciones derivables los extremos relativos tienen derivada 0, aunque no todos los puntos con derivada 0 son extremos relativos.

Los puntos de inflexión son puntos donde la función cambia de un tipo de concavidad a otro. En funciones derivables dos veces tienen derivada segunda 0, aunque tampoco que la derivada segunda sea 0 es sinónimo de punto de inflexión.

$$\begin{align}&f(x)=\frac{x^2-2x+1}{x+1}\\&\\&f'(x)=\frac{(2x-2)(x+1)-(x^2-2x+1)}{(x+1)^2}=\\&\\&\frac{2x^2+2x-2x-2-x^2+2x-1}{(x+1)^2}=\\&\\&\frac{x^2+2x-3}{(x+1)^2}\\&\\&\\&f''(x)=\frac{(2x+2)(x+1)^2-(x^2+2x-3)·2(x+1)}{(x+1)^4}=\\&\\&\frac{2(x+1)^2-2(x^2+2x-3)}{(x+1)^3}=\\&\\&\frac{2x^2+4x+2-2x^2-4x+6}{(x+1)^3}=\\&\\&\frac{8}{(x+1)^3}\\&\\&\text{Qué bien ha quedado, haremos la tercera}\\&\\&f'''=-\frac {24}{(x+1)^4}\\&\\&\text{Veamos los puntos donde }f'(x)=0\\&x^2+2x-3=0\\&\text{es fácil factorizarla de cabeza, sino usa}\\&\text{la ecuación de segundo grado}\\&(x+3)(x-1)=0\\&\text{Luego son los puntos -3 y 1}\\&\\&\text{Veamos el signo de la derivada segunda en ellos}\\&\\&f''(-3)= \frac{8}{(-3+1)^3}=\frac{8}{-8}=-1\lt0\implies máximo\\&\\&f(1)=\frac{8}{(1+1)^3}=\frac 88=1\gt0 \implies mínimo\\&\\&\text{El máximo relativo es }\\&f(-3)=\frac{9+6+1}{-3+1}=-\frac{16}{2}=-8\\&\text{luego el punto (-3,-8) es máximo relativo}\\&\\&\text{El mínimo relativo es}\\&f(1)=\frac{1-2+1}{1+1}=0\\&\text{Luego (1,0) es un mínimo relativo}\\&\\&\text{Ahora veamos los punto de inflexión }f''(x)=0\\&\\&\frac{8}{(1+x)^3}=0\\&\\&\text{No hay}\end{align}$$

El que no haya puntos de inflexión no significa que sea siempre del mismo tipo de concavidad, ya que hay un punto x=-1, donde la función no es ni continua ni derivable y eso hace que pasen cosas raras.

Y para graficar se necesitaría algún dato más, que citaré someramente ya que no los piden

El dominio de la función es todo R menos el punto x=-1

Hay un asintota vertical en x=-1

Solo hay un corte con el eje X ya que

(x^2 - 2x - 1) = (x-1)^2=0  ==> x=1

Eso de que sea un punto doble hace que en x=1 la funcion sea tangente al eje X.

El corte con el eje Y es (0, 1)

El límite en -infinito es -infinito

El límite en + infinito es +infinito

El límite en -1 por la izquierda es -infinito

El límite en -1 por la derecha es + infinito

Ah, y hay asíntota oblicua, ya que la función dividida por x tiene límite 1 en el infinito. Ese 1 es la pendiente y el valor de b es

$$\begin{align}&\lim_{x\to \infty}(f(x)-mx)=\\&\\&\lim_{x\to \infty}\left(\frac{x^2-2x+1}{x+1}-x  \right)=\\&\\&\lim_{x\to \infty}\left(\frac{x^2-2x+1-x^2-x}{x+1} \right)=\\&\\&\lim_{x\to \infty}\left(\frac{-3x+1}{x+1} \right)=-3\\&\\&\text{Luego la asíntota oblicua es}\\&\\&y=x-3\end{align}$$

Y he hecho muchas cosas para la gráfica, pero será un programa el que la haga

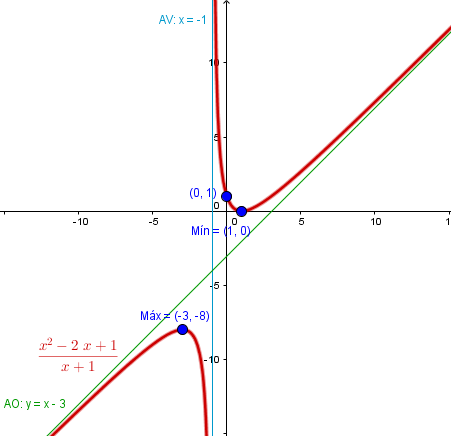
Y eso es todo, espeero que te sirva. Y recuerda lo de votar a quien se lo merece, no a los buscadores de Google que no hacen otra cosa.

En este mundo siempre estamos los que trabajamos y los aprovechados. Espero sepas distinguir unos de otros y valores lo que realmente merece la pena y desprecies lo que no.

Ana Belen. Me ofendes si puntúas las respuestas de Jorge Herrera. ¿Tiene algo que ver lo que hace él con el trabajo que he hecho yo? ¿Le vas a puntuar todas las veces por mandarte esos vídeos? ¡Vaya chollo! ¿Sabes qué estás votando a un analfabeto matemático que no ha resuelto todavía ni un solo problema? Como no le retires estos votos ya no cuentes con ninguna respuesta más mía.