Usando el Método de la Regla Falsa aproximar la raíz de
____________________________________________________________________________
2 respuestas
·
·
¡Hola Juan David!
Qué habilidad tan grande tiene Herrera par buscar por Internet. Si dedicará una mínima parte de ella a aprender podría contestar las pregunatas en vez de mandar enlaces que no cuesta nada conseguirlos. No tienes porque aguantar sus respuestas, puedes bloquearlo.
El método de la regula falsa es un pequeño avance respecto del método de bisección que converge muy lento.
En la iteración k tendremos la raíz dentro de un intervalo
$$\begin{align}&[a_k, b_k]\\&\\&\text{Tomaremos el valor}\\&\\&c_{k}=\frac{f(b_k)·a_k-f(a_k)·b_k}{f(b_k)-f(a_k)}\\&\\&\text{Como ves esto son más cuentas que con la}\\&\text{bisección e invita ausar al menos una hoja de}\\&\text{Excel para completarlo}\\&\\&\text{Haré solo un par de iteraciones a mano}\\&\text{Tenemos }[a_0, b_0]=[0,1]\\&\\&\text{Antes de nada veamos donde es positiva o}\\&\text{negativa la función, en 0 se calcula de un vistazo}\\&\\&f(0)=-0.5\\&f(1)= 0.8912085469\\&\\&\text{Luego deberemos dejar siempre a la izquierda}\\&\text{un valor que haga negativa a f y a la derecha positiva}\\&\\&c_0=\frac{f(1)·0-f(0)·1}{f(1)-f(0)}=\\&\\&\frac{-e^0(3.2·0-0.5·1)}{e^{-1}(3.2sen(1)-0.5cos(1))-e^0(3.2·0-0.5·1)}=\\&\\&\frac{0.5}{e^{-1}(3.2sen(1)-0.5cos(1))+0.5}=\\&\\&=0.3593997472\\&\\&f(c_0)=f(0.3593997472)=0.4589456850595\\&\text{Que es mayor que el error permitido}\\&\\&Como\; f(c_0)\gt 0 \text{ debe ir a la derecha en el}\\&\text{próximo intervalo, luego será:}\\&\\&[a_1, b_1]=[0, \;0.3593997472]\end{align}$$Y estas cuentas a mano son muy pesadas y te puedes equivocar, luego voy ya a confeccionar la hoja de Excel.
Estos son los resultados:
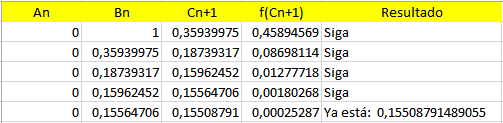
Y esta es la hoja por si el diseño te puede servir para hacer otros, aunque hay que trabajar un poquito y saber Excel, no es automático su uso.
https://drive.google.com/file/d/0B3nG6r7qbZZ_bUZkeEpxbGtOa0U/view?usp=sharing
Y ya está, espero que te sirva y si no entiendes algo me lo dices.
Salu_dos.
¡Ah hola Herrera, aquí como siempre esperando a ver si cae algo de carroña, haces bien, tú si que sabes!
:
:
Aquí te dejo unos enlaces para que encuentres la respuesta:
http://es.slideshare.net/asesoracademico/03-metodo-de-regla-falsa
https://www.youtube.com/watch?v=1eCpfwauaAQ
http://www.buenastareas.com/materias/m%C3%A9todo-de-regla-falsa-ejercicios-resueltos/0