Aplicando las reglas de derivación calcular de calculo diferencial
Me ayudan por favor con el siguiente ejercicio de derivación
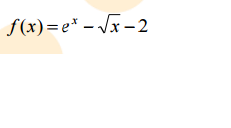
3 respuestas
Respuesta
1
Respuesta de Lucas m
1
Respuesta de Valero Angel Serrano Mercadal
1
