Hallar la ecuación de la circunferencia de radio 13 que es tangente a la circunferencia x^2+y^2-4x+2y-20=0 en el punto P(2,4)
Lo primero que realice fue sacar el centro y el radio de la circunferencia, que es centro:(2,-1) y radio: 5
·
·
¡Hola Anyara!
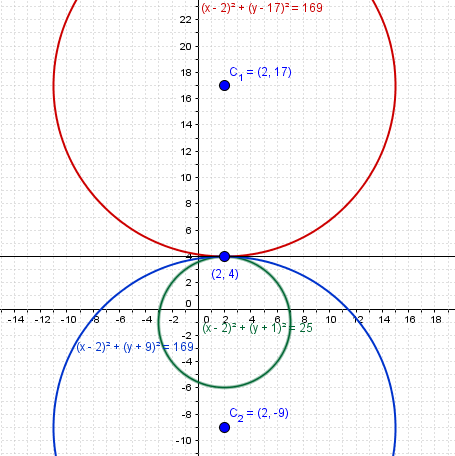
Has calculado bien el centro (2,-1) el radio no es necesario saberlo.
Si dos circunferencias son tangentes la recta que une sus centros pasa por el punto de tangencia.
Calculemos el vector que va del centro de la conocida al punto de tangencia
(2, 4) - (2, -1) = (0, 5)
Que bien, aun más sencillo, vamos a tomar el vector de esa dirección que mide 13
v=(0,13)
Y ahora lo que tenemos que hacer es calcular el centro de la circunferencia añadiendo ese vector y su inverso al punto de tangencia, por que hay dos circunferencias tangentes una a cada lado de la tangente.
El centro de la primera será
(2, 4) + (0,13) = (2,17)
Y su circunferencia es
(x-2)^2 + (y-17)^2 = 13^2
Y la otra tiene centro en
(2, 4) - (0, 13) = (2, -9)
y es
(x-2)^2 + (y+9)^2 = 169
vamos a comprobarlo todo.
Y eso es todo, saludos.
:
:
