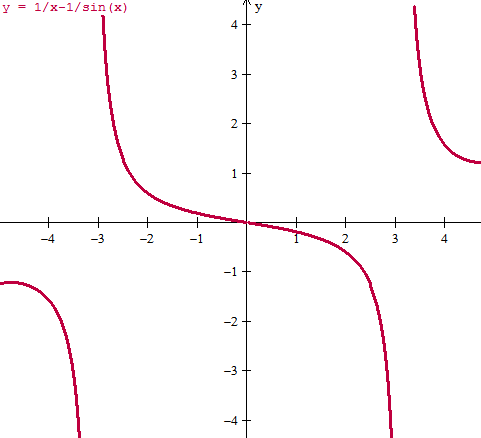Este limite Por L. Hospital me da infinito
Tengo el siguiente límite:
$$\begin{align}&\lim_{x \to 0} \frac{1}{x} - \frac{1}{senx}\end{align}$$Al momentop de aplicarle varias veces Hopital a lo último me da 1/0, lo que da infinito, tengo que hallar el límite por hopital o por otro método, pero este no funcionó...
1 Respuesta
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Carlos!
X y senx tienen el mismo orden cuando tienden a 0, luego lo lógico es que el límite valiese 0.
$$\begin{align}&L=\lim_{x\to 0} \left(\frac 1x - \frac 1{senx}\right)=\\&\\&\lim_{x\to 0} \frac{senx-x}{x·senx}= \frac 00\\&\\&\text{aplicamos l'Hôpital}\\&\\&L= \lim_{x\to 0} \frac{cosx-1}{senx+x·cosx}= \frac {1-1}{0+0}= \frac 00\\&\\&\text{Lo aplicamos otra vez}\\&\\&L=\lim_{x\to 0} \frac{-senx}{cosx+cosx-x·senx}=\frac 0{1+1+0}=0\end{align}$$Y aquí tienes la confirmación gráfica:
Y eso es todo, saludos.
:
:
