Inicialmente un cultivo tiene un número 𝑃𝑜 de bacterias. En 𝑡=1 ℎ se determina que el número de bacterias es 4/3 𝑃𝑜.
Si la razón de crecimiento es proporcional al número de bacterias𝑃(𝑡) presentes en el tiempo t, determine el tiempo necesario para que se duplique el número de bacterias.
Solución a evaluar:
Planteando la ecuación diferencial sería:
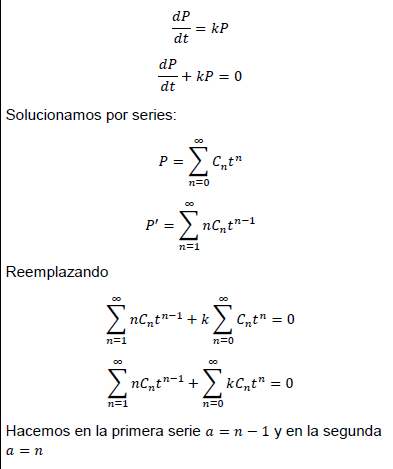
Necesito encontrar el error de esta solución.
1 Respuesta
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Juan David!
No hay fallo en la solución, la función P(t) obtenida es correcta y la población se duplica en 2.41 h tal como dicen.
Si acaso se podría dejar mejor la función
P(t) = Po·(4/3)^t
Al principio hay un fallo:
dP/dt = kP
dP / dt - kP = 0
que luego queda compensado porque cuando llegan a
$$\begin{align}&C_{a+1}=- \frac{kC_a}{a+1}\\&\\&\text{luego dicen}\\&\\&P=\sum_{n=0}^{\infty}C_0 \frac{k^nt^n}{n!}\\&\\&\text{que es donde se corrige el fallo. Porque}\\&\text{la continuación lógica era}\\&\\&P=\sum_{n=0}^{\infty}C_0 (-1)^n \frac{k^nt^n}{n!}\end{align}$$Luego hay dos fallos que se compensan entre sí para que al final no haya fallo.
Y eso es todo, saludos.
:
:
