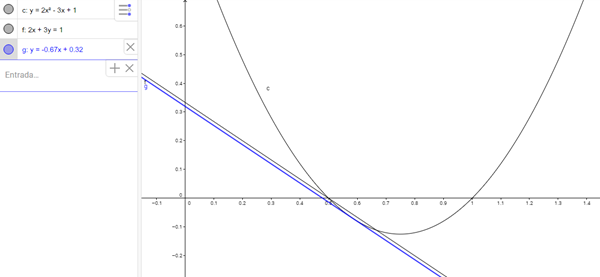
Encuentre las coordenadas del punto donde la recta tangente a la curva w=2r^2-3r+1, es paralela a la recta 2r+3w−1=0
Puedo sacar la pendiente sacando la derivada de la curva, donde también se que esa misma pendiente es la misma de la otra recta, pero luego no se que hacer, ayuda!
1 respuesta
veamos que sale...
Primero voy a escribir la recta en la forma "principal"
w = -2/3 r + 1/3
la derivada de la curva es
w'(r) = 4r - 3
Tenemos que ver en que punto esa derivada vale lo mismo que la pendiente de la recta (-2/3)
-2/3 = 4r - 3
-2/3 + 3 = 4r
7/3 = 4r
r = 7/12
En ese punto la curva vale
w=2(7/12)^2 - 3 (7/12) + 1 = - 5/72
Por lo tanto la ecuación de la recta tangente paralela tiene pendiente -2/3 y sabemos que pasa por el punto (7/12, -5/72), así que
-5/72 = -2/3 (7/12) + b
b = -5/72 + 14/36
b = 23/72
y la ecuación es
w_2 = -2/3 r + 23/72
Te dejo la imagen (en azul el resultado, considerá para el gráfico que lo que para vos es (r, w), en el gráfico sería (x, y))
Salu2