Tablas de verdad y leyes de inferencia, Lógica Matemática
Demostrar la validez o no validez del argumento dado a través de
- Uso de las reglas de inferencia.
- Uso de las tablas de verdad.
Este es el enunciado:
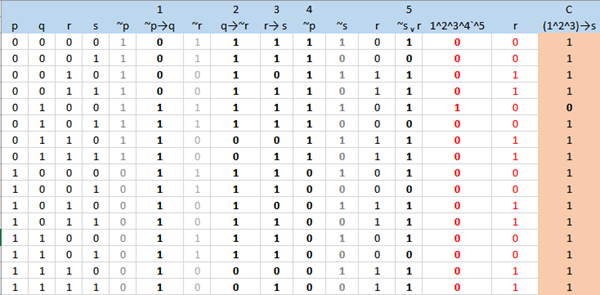
“Si no compramos una parcela, entonces construimos una casa. Si construimos una casa, no compramos un apartamento. Si no compramos un apartamento entonces compramos muebles. No compramos una parcela. No compramos muebles o compramos un apartamento. Por lo tanto, compramos un apartamento”
1 respuesta
·
·
¡Hola Jhon!
Veamos a ver que este no lo he cogido a la primera.
p= Compramos una parcela
q = Construimos una casa
r = Compramos un apartamento
s = Compramos muebles
Y el razonamiento es
1) ~p ==> q
2) q ==> ~r
3) r ==> s
4) ~p
5) ~s v r
C) r
Por 4) y 1) por modus tollens tenemos
6) q
Y ahora por modus tollens de 6) y 2) tenemos
7) ~r
Y por la regla del silogismo disyuntivo entre 7) y 5) tenemos
8) ~s
Y por modus tollens en 3) tenemos
9) ~r
Luego el razonamiento está mal es lo contrario de lo que tenía que dar
Veámoslo con la tabla de la verdad:
[(~p ==> q) ^ (q ==> ~r) ^ (r ==> s) ^ ~p ^ (~s v r)] ==> r
Y eso es todo, sa lu dos.
:
:
Ah, se me olvidó decir que hay un cero en la tabla de la verdad, por eso está mal el razonamiento.
