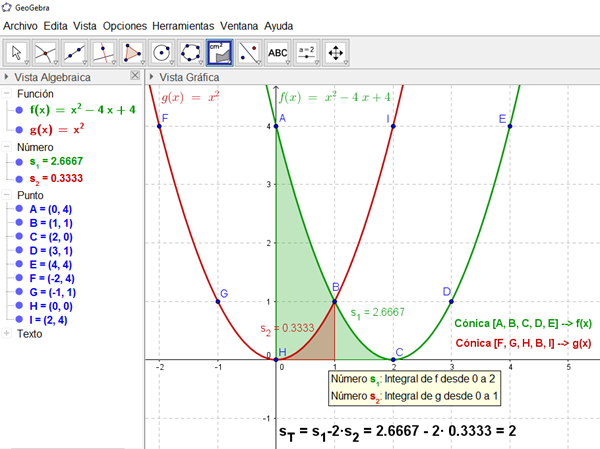
Encontrar las ecuaciones de la curva
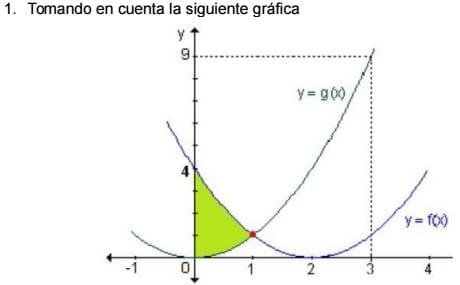
De la imagen anterior determinar las ecuaciones de la curva y el área sombreada
3 Respuestas
Respuesta de Enrique Ezpeleta
2
Respuesta de Lucas m
1
Respuesta de Valero Angel Serrano Mercadal
1