Obtener una raíz de la función f(x) = Cos (x+1) – Sen (x+1) + 0.8 en el intervalo [0,1] por el métodode la secante.

·

·

¡Hola Luk!

Es horrible todo lo que hay que escribir y calcular, luego lo haré todo ayudado por Máxima. Te pondré todo el desarrollo de los dos primeros pasos, pero después no

El método de la secante es:

$$\begin{align}&x_{n+1}= x_n- \frac{x_n-x_{n-1}}{f(x_n)-f(x_{n-1})}f(x_n)\\&\\&\\&x_{n+1}= x_n- \frac{(x_n-x_{n-1})(\cos(x_n+1)-sen(x_n+1)+0.8)}{\cos(x_n+1)-sen(x_n+1)+0.8-\cos(x_{n-1}+1)+sen(x_{n-1}+1)-0.8}\\&\\&x_{n+1}= x_n- \frac{(x_n-x_{n-1})(\cos(x_n+1)-sen(x_n+1)+0.8)}{\cos(x_n+1)-sen(x_n+1)-\cos(x_{n-1}+1)+sen(x_{n-1}+1)}\\&\\&\\&\text{empezaremos con }\\&x_0=0\\&x_1=1\\&\\&x_2= 1- \frac{(1-0)(\cos(1+1)-sen(1+1)+0.8}{\cos(1+1)-sen(1+1)-\cos(0+1)+sen(1+0)}=0.4870088954979285\\&\\&x_3=0.4870088954979285-\frac{(0.4870088954979285-1)(\cos(0.4870088954979285+1)-sen(0.4870088954979285+1)+0.8)}{\cos(0.4870088954979285+1)-sen(0.4870088954979285+1)-\cos(1+1)+sen(1+1)}=\\&\\&0.3467743003058448\\&\\&x_4=0.3881064627241549\\&\\&x_5=0.3866815182903999\\&\\&x_6=0.3866623705856034\\&\\&\text{Creo que decían hasta aquí}\\&\text{El resultado con 4 decimales es: }0.3867\end{align}$$

Y el método usado con Maxima por si quieres usarlo ha sido:

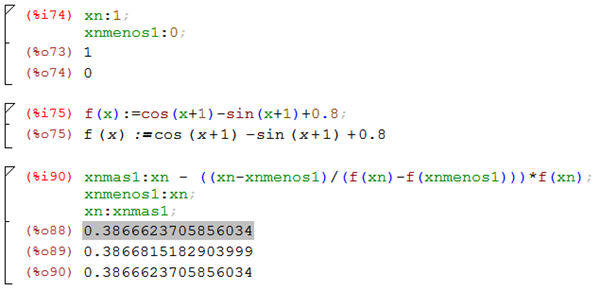
Primero se conmutó a salida numérica, luego se ejecuto (%i74), luego (%i75) y después cada vez que se ejecuta (%i90) se obtiene una iteración.

También podría hacerse mejor con Excel ahora que lo pienso.

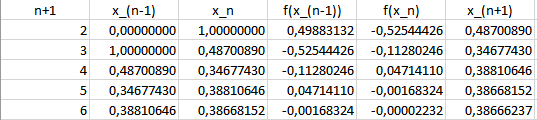
Aqui tienes la hoja de cálculo para que la puedas revisar y emplear para otros casos cambiando lo que haya que cambiar: Hoja de Excel del método de la secante

Y eso es todo, sa lu dos.

:

: