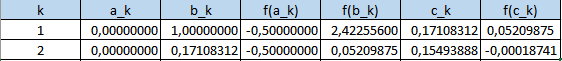Usando el Método de la Regla Falsa aproximar la raíz de f(x)= e^(-x) (3,2sen(x)-0,5cos(x)) en el intervalo [0, 1] con ξa = 0

·

·

¡Hola Luk Dary!

El método de la regla falsa es:

$$\begin{align}&c_k=\frac{f(b_k)a_k-f(a_k)·b_k}{f(b_k)-f(a_k)}\\&\\&\text{Si }c_k\text{es suficientemente pequeño ya está}\\&\\&\text{Si no, se toma como nuevos extremos } c_k \text{ y el valor }\\&a_k\; o\; b_k \text{ que tenga signo opuesto a }c_k\\&\text{Según sea eso puede darse}\\&[a_{k+1},b_{k+1}]=[a_k, c_k]\\&o\\&[a_{k+1},b_{k+1}]=[c_k,b_k]\\&\\&\text{Empezamos con }\\&a_1=0;b_1=1\\&\\&c_1= \frac{(3.2 sen1-0.5cos1)·0-(3.2sen0-0.5cos0)·1}{(3.2 sen1-0.5cos1)-(3.2sen0-0.5cos0)}=\\&\\&\frac{0.5}{2.922555998}=0.170831205\\&\\&Tenemos\\&f(a_1)=f(0)=-0.5\\&f(c_1)= f(0.170831205) = 0.05209875\gt0.001\\&f(b_1)=f(1)=2.42255600\\&\\&\\&\text{Para que haya signos distintos de la función se debe tomar}\\&[a_2,b_2]=[0, \;0.170831205]\\&\\&c_2= \frac{(3.2 sen0.170831205-0.5cos0.170831205)·0-(3.2sen0-0.5cos0)·1}{(3.2 sen0.170831205-0.5cos0.170831205)-(3.2sen0-0.5cos0)}=\\&\\&0.15493888\\&\\&Tenemos\\&f(a_2)=f(0)=-0.5\\&f(c_2)=f(0.15493888)=-0.00018741\\&|f(c_2)|=0.00018744 \lt 0.001\\&\\&\text{Entonces ya está}:\\&\\&x=0.15493888\end{align}$$

Las cuentas las hice con Excel por supuesto, hay cuentas que ya da pereza hacer con calculadora.

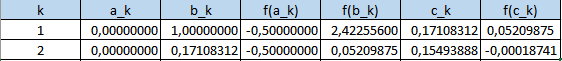
Y puedes encontrar los dos métodos aquí: Hoja de cálculo, métodos calcular raíces

Se podría mejorar la hoja con macros para que ella sola hiciera las cuentas necesarias hasta obtener un error menor, pero ya está bastante bien así, tu copias la ultima fila cuantas veces necesites abajo según la solución requiera más o menos iteraciones.

Saludos.

:

:

¡Gracias!