Hallar área de un circulo

El área que te está pidiendo el ejercicio depende del valor que le des a la longitud "a" y "b", la ecuación que te da el problema se puede escribir de la sig. manera:

Ya que siendo un círculo, necesariamente a=b ya que para todo ángulo, el radio permanece constante, entonces igualando "b" por "a" y simplificando:

$$\begin{align}&\frac{X^2}{a}+\frac{Y^2}{a }⇒    \frac{X^2+Y^2}{a}=1\end{align}$$

   Pasando "a" al otro lado de la ecuación:

$$\begin{align}&X^2+Y^2=a\end{align}$$

  Convenientemente nos ha quedado en la forma de la identidad fundamental Pitagórica

$$\begin{align}&sen^2(x)+\cos^2(x)=1\\&\end{align}$$

  Para comprobarlo, vamos a hacer X=sen(x)=hyp/ady y Y=cos(x)=hyp/op

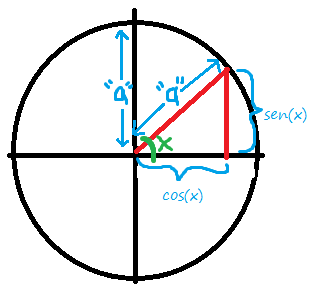
Entonces nuestro X=cos(x)/a, y nuestro Y=sen(x)/a, al meter ambos valores en nuestra ecuación queda:

$$\begin{align}&(\frac{\cos(x)}{a})^2 + (\frac{sen(x)}{a})^2= r^2\end{align}$$

Multiplicamos la ecuación por "a²" para eliminarlo del lado izquierdo, y nos queda:

$$\begin{align}&\cos^2(x) + sen^2(x)=\frac{1}{a^2}\end{align}$$

Pero resulta que a=r=1, por lo que nuestra ecuación se redujo nuevamente a la identidad fundamental Pitagórica, por lo tanto el área del círculo es una función de "a", en otras palabras, el área del círculo depende del valor dado al radio "a".