Cual es la suma de las cifras del número original ?
Si el complemento aritmético de un número capicúa de 5 cifras es otro capicúa de 4 cifras, hallar la suma del número original
Respuesta de Luis Alberto Candio Salcedo
1
1 respuesta más de otro experto
Respuesta de Lucas m
1

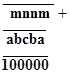

Muy buena la deducción pero a=9. Salu2 - Anónimo
Si tienes razón, gracias por la observación.............. - Luis Alberto Candio Salcedo