¿Cuánto tiempo transcurrirá para que la corriente alcance a) 50.0% y b) 90.0% de su valor final?
Una batería de 9𝑉 está conectada en un circuito en serie que contiene un resistor de 12Ω y un inductor de 4𝐻. ¿Cuánto tiempo transcurrirá para que la corriente alcance a) 50.0% y b) 90.0% de su valor final?
1 respuesta
La corriente que se te establece será del tipo transitorio valiendo 0 al principio y creciendo gradualmente hasta un valor permanente.
La ecuación que rige esta corriente es del tipo exponencial y se expresa:
i(t) = V/R ( e^-R/L)(t )..................R/L = constante de tiempo del circuito.
En este caso: i(t) = 9/12 ( e^-12/4) = 0.75 ( e^-3t) A.
Para que la corriente llegue al 50 % de la permanente = 0.75 A. se necesitara un tiempo to :
0.50 x 0.75 = 0.375 A
I( 50%) = 0.375 = 0.75( e^-3 to) ..........................0.50 = e^-3 to ..........-3 to = ln ( 0.50 ) = -0.6931 ....................to= -3 / -0.6931 = 4.32 s.
i( 90%)...............lo obtendrias de resolver 0.90 = e^-3ti.................-3 / -0.10536 = 28.473 s.
Aclaración:
La respuesta correcta es la que sigue:
La corriente que se te establece será del tipo transitorio valiendo 0 al principio y creciendo gradualmente hasta un valor final permanente.
La ecuación que rige esta corriente es del tipo exponencial y se expresa:
i(t) = V/R ( 1 - e^-(R/L)t )..................L/R =0.33 s= constante de tiempo del circuito.
En este caso: i(t) = 9/12 ( 1 - e^-12/4 t ) = 0.75 ( 1 -- e^-3t) A.
Para que la corriente llegue al 50 % de la permanente = 0.75 A. se necesitara un tiempo to :
50 % Corriente final :0.50 x 0.75 = 0.375 A
I( 50%) = 0.375 = 0.75( 1 - e^-3 to) ..........................( - 0.50) = - e^-3 to .........
to= ln(0.50) / (-3) = 0.23 s.
Para el caso del 90% de la corriente final procedes igual y obtendrías un tiempo logicamente mayor.
Gráfico de corriente como función del tiempo en segundos.
.
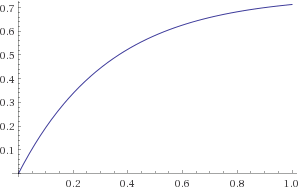
Sinceramente creo que Albertx se ha equivocado, pues si la constante de tiempo es L/R = 4/12 = 1/3 = 0,33s, que es el tiempo en el que la corriente alcanza el 66,2% de la final de 9/12 = 0,75A, al 50% debe ser inferior. A mi me sale 0,23s y para el 90% de 0,76s. Saludos - Botijo Antiguo
Si señor... justamente acabo de hacer la corrección correspondiente... - albert buscapolos Ing°