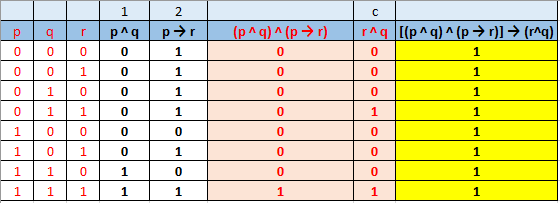
Planteamiento y resolución aplicando tablas de verdad y leyes de inferencia, simulador truth
Desde muy joven empecé a trabajar para poder buscar tener una buena calidad de vida, pero siempre me fue complicado poder ingresar a hacer mis estudios superiores; hoy en día afortunadamente la UNAD ofrece una excelente oportunidad de formación académica para quienes tenemos una vida laboral muy densa, pues la virtualidad, aunque demanda de disciplina y adecuados hábitos de estudio, nos permite contar con las 24 horas del día, los siete días de la semana para ingresar a realizar las actividades según las fechas límites establecidas; esto es algo que me ha alegrado mucho y le hice el siguiente comentarios a mis amigos, para que se motiven e ingresen a estudiar en la UNAD: “ He ingresado a estudiar administración en salud y lograré materializar mi proyecto de vida. Si he ingresado a estudiar en la UNAD administración en Salud, entonces conseguiré un mejor estatus laboral. Por lo tanto, conseguiré un mejor estatus laboral y lograre materializar mi proyecto de vida”. Por medio de los diferentes métodos de demostración con las tablas de verdad y el uso de las leyes de inferencia, determinar si mi razonamiento es válido.
Aplicar:
- Tablas de verdad.
- Leyes de inferencia
- Simulador Truth.
Salu2
1 Respuesta
Es un ejercicio muy sencillo, por supuesto que el razonamiento es válido, se ve desde lejos.
p = He ingresado a estudiar administración en salud
q = lograré materializar mi proyecto de vida
r = conseguiré un mejor estatus laboral
Y las proposiciones compuestas que nos dan son
1) p ^ q
2) p -> r
siendo la conclusión
c) r ^ q
Por las reglas de inferencia tenemos que por simplificación conjuntiva en 1 se cumplen
4) p
5) q
Por 4) y modus ponens en 2) se cumple
6) r
Y por 6) y 5) se cumple
c) r ^q
-------------------
Por tabla de verdad habría que demostrar que
[(p ^ q) ^ (p -> r)] -> (r ^ q)
----------------------------
Y con el simulador es lo mismo de arriba pero con otra notación:
[(p & q) & (p > r)] > (r & q)
Y eso es todo, sa lu dos.
:
:
