Realizar el siguiente problema de programación lineal pro el método simplex

·

·

¡Hola Oscar!

El propio enunciado te dice los pasos para plantear el problema, pero en el mimento que solo añade una variable de holgura falla.

El problema es maximizar

Z = 50000X1 + 40000X2

con las restricciones

X1 + 1.5X2 <= 750

2X1 + X2 <= 1000

X1, X2 >= 0

Añadiremos una variable de holgura S1 en la ecuación primera y otra S2 en la segunda. Asímismo ponemos la ecuación de Z ya igualada a 0 que es como irá en la tabla que usaremos.

X1 + 1.5X2 + S1 = 0

2X1 + X2 + S2 = 0

Z - 50000X1 - 40000X2 = 0

Estos datos se pasan a la tabla, hay mil formas de poner las columnas luego atento a cómo las puse yo tal como las vi en este vídeo https://www.youtube.com/watch?v=FhBC9LaTjQY

Una vez puestos se elige la columna pivote que es la que tiene mayor valor negativo en la fila Z, en este caso será -50000, luego en última columna se divide cada elemento de la columna solución entre el correspondiente de la columna pivote, y el que dé un valor positivo menor será la fila pivote, en este caso será 500, con ello el elemento pivote será 2.

La variable entrante es la de la columna pivote X1 y la saliente es la de la fila pivote S2. En la columna de variables básicas haremos ese cambio y dividiremos la fila pivote entre el pivote.

Ahora a la fila S1 le restaremos la fila pivote multiplicada por el valor de S1 en la columna pivote. Como ese valor es 1 es simplemente restar, es decir, haremos:

S1 = S1-X1

Hacemos lo mismo para la fila Z, como el elemento de la columna pivote es (-50000) el restar la fila X1 multiplicada por (-50000) es lo mismo que sumar la fila X1 multiplicada por 50000

Z=Z + 50000X1

Vemos que en la fila Z hay un valor negativo, eso significa que no hemos terminado aun y tenemosq ue hacer lo mismo que hicimos antes tomando como columna pivote la X2. Dividimos la columna solución entre la columna de X2 y vemos que el valor positivo menor es el de la fila S1.

La variable que entra es X2 y la que sale S1. No es necesario dividir la fila pivote ya que tiene valor 1 el pivote. Así que la imagen que pondré ya tiene el siguiente paso que es restar a la fila X1 la X2 multiplicada por 0.5

X1 = X1 - 0.5X2

Y con la fila Z se hace lo mismo, como esu elemento pivote es -15000 la operación es sumar 15000 veces la columna X2

Z= Z + 15000X2

Y ya no hay elementos negativos en la fila Z, por lo tanto hemos terminado. La solución es:

X1 = 375

X2 = 250

Z = 28750000

Hacemos una mera comprobación que la solución es compatible

Z = 50000*375 + 40000*250 = 28750000

Eso está bien, pero para asegurarnos de que esa es la mejor respuesta posible usamos el programa PHPSimplex y enla última pantalla tenemos

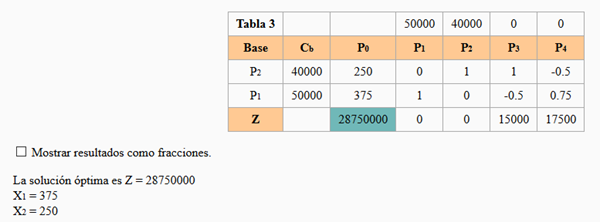
Que es lo mismo que hemos calculado a nuestra manera.

Y eso es todo, sa lu dos.

:

: