El àrea del circulo inscrito en el hexàgono regular es 25pi, entonces el àrea de la parte sombreada es :
La respuesta que da el libro es B) (50√3) - 25pi, pero a mi me da (75√3/2) - 25pi, ¿qué tendrè mal?

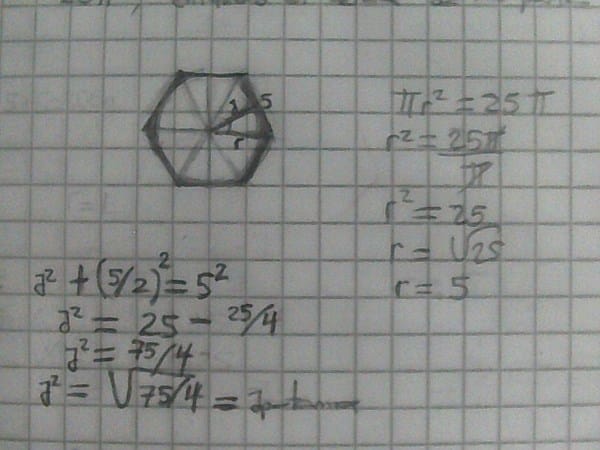

1 respuesta
Respuesta de Lucas m
1
