Anónimo
Matemáticas: Diversas poblaciones de animales, entre ellas la de conejos...
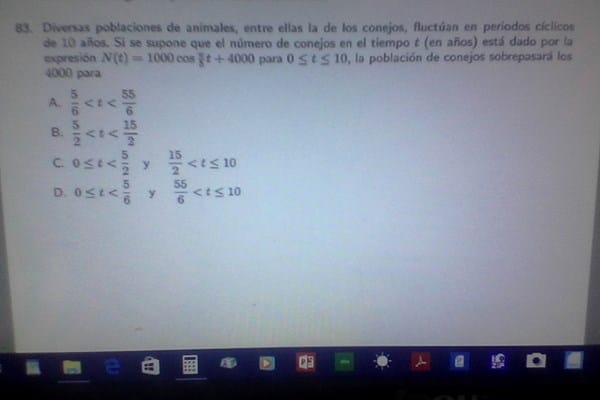
Diversas poblaciones de animales, entre ellas la de conejos, fluctúan en periodos cíclicos de 10 años. Si se supone que el numero de conejos en el tiempo t ( años) esta dado por la expresión :
N(t) = 1000 cos pi/5 t + 4000, para 0 ≤ t≤ 10, la poblaciòn de conejos sobrepasarà los 4000 para ( ver la segunda imagen).
Tratè de desarrollarlo pero lleguè hasta acà, gracias por la explicaciòn.
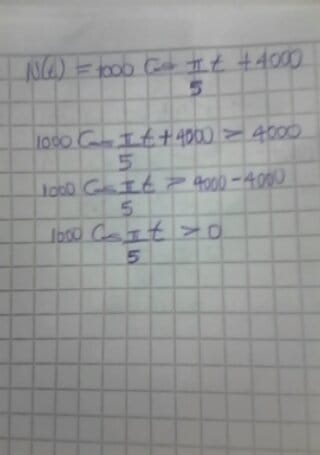
2 respuestas
Lo que hiciste está bien, voy a continuar a partir de tu punto...
$$\begin{align}&1000 \cos( \frac{\pi}{5} t) > 0\\&\cos( \frac{\pi}{5} t) > \frac{0}{1000}\\&\cos( \frac{\pi}{5} t) > 0\\&\text{Sabemos que el \cos(t) es > 0 para t entre 90° y -90° que expresado en radianes }\\&\text{podríamos decir que es } \pi/2 < t < -\pi/2, \text{ pero que tambien podemos expresar como } 3/2 \pi < t < 5/2 \pi\\&\text{Ahora expresemos ese valor en función a lo que tenemos} \\& 3/2 \pi < \frac{\pi}{5} t < 5/2 \pi\\& 15/2 < t < 25/2 \\& \text{Ese es el rango donde 'se mueve' el \cos > 0, pero como a su vez, t está en el intervalo [0, 10], la respuesta es:}\\& 15/2 < t \le 10\end{align}$$Viendo las opciones, veo que lo más parecido es la C, pero a mí me falta la opción 0 < t < 5/2, que analizando un valor cualquiera de ahí se verifica que también vale, por lo que seguramente en mi despeje olvidé algo, (pero en este momento no tengo tiempo de revisarlo)
Salu2
Muchas gracias por la explicaciòn.
Me alegro que te haya servido.
Salu2
La respuesta es la C.
Como bien decía Gustavo el cos de x es positivo en los intervalos 0 - pi/2 y 3pi/2 - 5pi/2
Vemos el valor de t en cada paso por cero: t*pi/5=0 luego t=0 ; t*pi/5= pi/2 luego t= 5/2; t*pi/5=3pi/2 luego t= 15/2; t*pi/5=5pi/2 luego t=25/2 (mayor de 10)
De manera que los intervalos de t serán: 0 - 5/2 y 15/2 - 10
No obstante, para ser estrictos yo dejaría los dos intervalos abiertos ya que pregunta por períodos en los que se "sobrepasará" los 4.000 conejos. Aunque eso siempre supondría discutir con el examinador y éste siempre tiene la razón... y si no la tiene hay que dársela :-)